Планиметрия на Изумруде

Пусть Обозначим середины сторон через соответственно, а длины медиан — через соответственно.

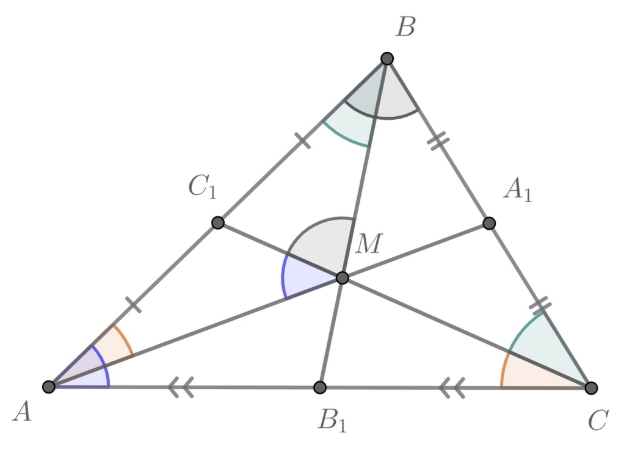
Заметим, что

Аналогично, Как известно, существует треугольник, стороны которого равны и параллельны медианам треугольника Построим треугольник такой, что

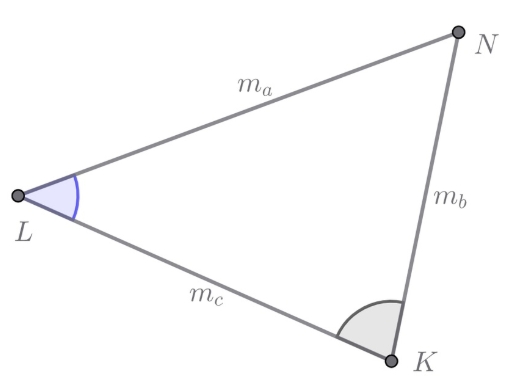
Углы этого треугольника будут равны углам между медианами а именно

и

Следовательно, треугольники и подобны по двум углам, а значит,

По формуле длины медианы треугольника получим

откуда

Первое равенство равносильно

откуда

Предположив, что , получим откуда Равенство

также выполняется, что проверяется прямой подстановкой.

Таким образом, под условие задачи подойдёт любой треугольник, длины сторон которого связаны соотношением например, треугольник со сторонами

Замечание. Треугольники, длины сторон которых связаны соотношением , называются автомедианнымии.