Планиметрия на Изумруде
Ошибка.
Попробуйте повторить позже
В остроугольном треугольнике 
отметил точку 
— середину стороны 
и точку 
пересечения высот. Оказалось, что
четырёхугольник 
— вписанный. В каком отношении высота 
делит сторону 
Источники:
Пусть 
и 
— основания высот 
и 
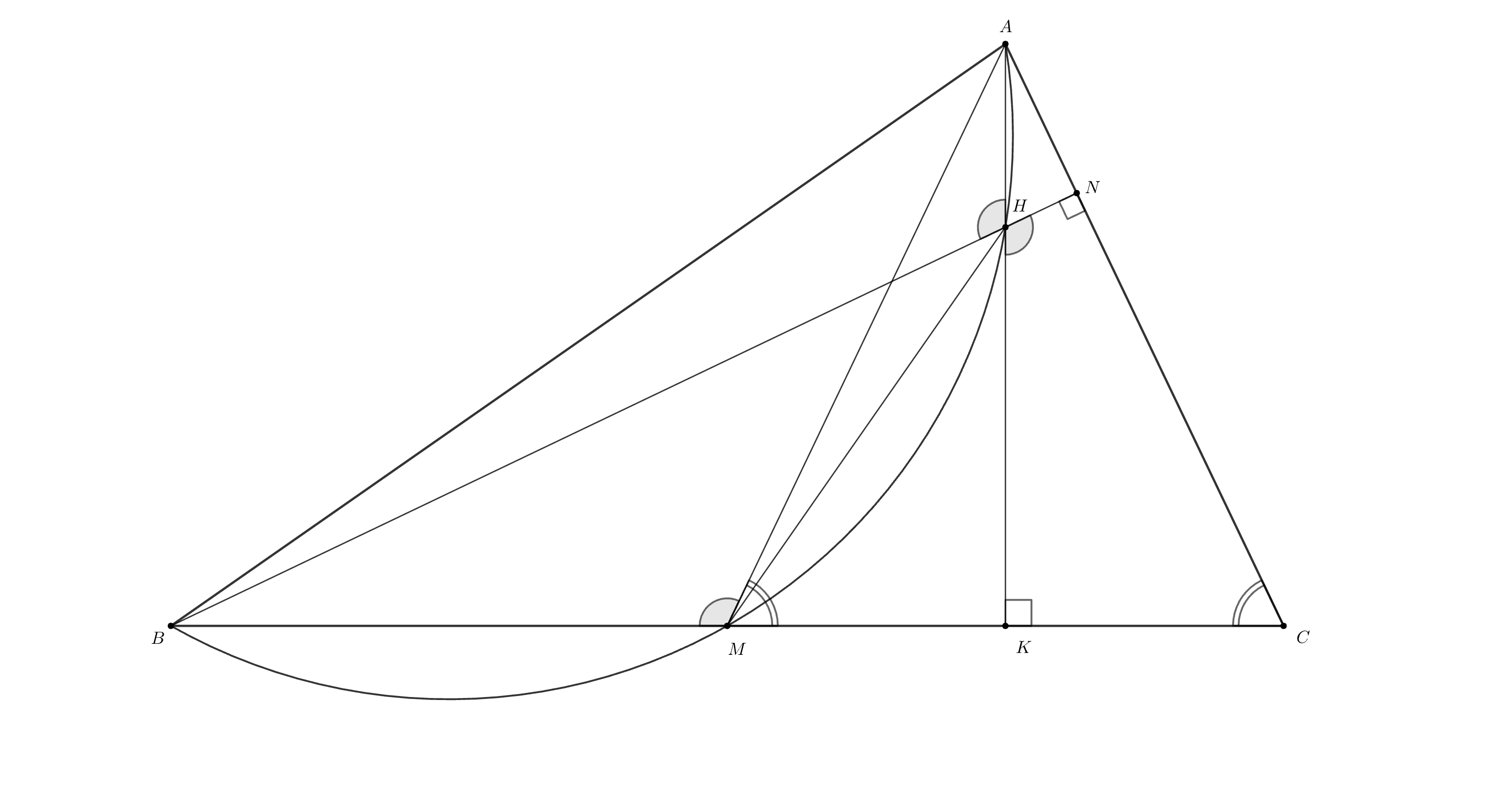
соответственно. По сумме углов в четырехугольнике 
Четырехугольник 
— вписанный, следовательно,
Кроме того,
Получим, что
Треугольник 
— равнобедренный, 
— высота, следовательно, и медиана. По условию, 
— середина 
Получим,
что
Специальные программы
Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!
Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.
Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.
Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».
Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!
Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!
