Увидеть треугольник

Первое решение.

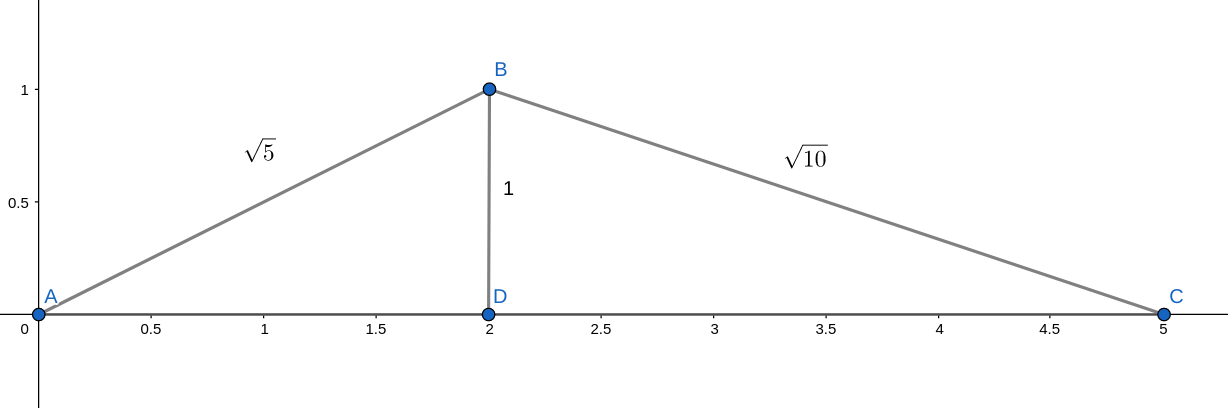
Отложим на оси координат от точки с координатами отрезок длины влево, длины вверх и длины вправо. Тогда В треугольнике по теореме косинусов Тогда . По теореме о сумме углов в треугольнике получаем, что , откуда следует

______________________________________________________________________________________________________________________________________________________

Второе решение. Сначала заметим, что . Кроме того, из-за области определения каждого арктангенса из суммы. По формуле тангенса суммы

Поскольку угол лежит на промежутке , то это единственное возможное значение. Отсюда сумма из условия равна .

_________________________________________________________________________________________________________________________________________________________________________________

Третье решение. Рассмотрим прямоугольник со сторонами и и построим из точки лучи с нужными тангенсами:

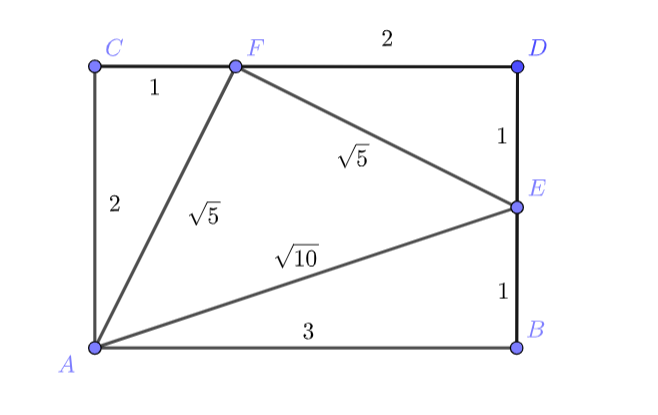
Заметим, что и , то есть осталось доказать, что (поскольку сумма всех трёх равна ). Но , так что по обратной теореме Пифагора , причём равнобедренный прямоугольный, откуда и следует нужное равенство.