Комбинаторика на Питергоре
Ошибка.
Попробуйте повторить позже
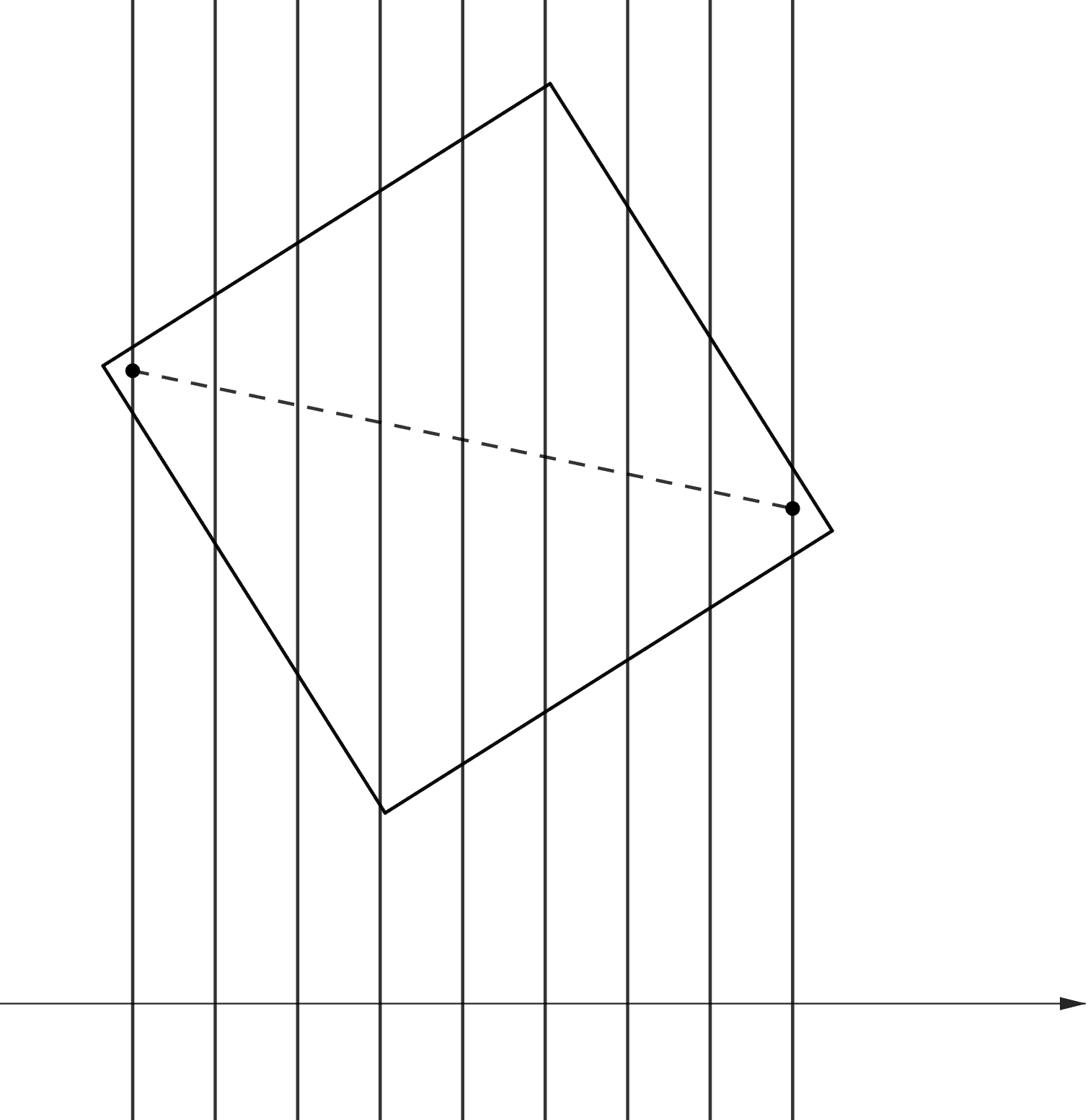
На клетчатую плоскость со стороной клетки, равной произвольным образом брошена салфетка
Она накрывает некоторые
узлы (узел, лежащий на границе салфетки, тоже считается накрытым). Каким наименьшим числом прямых (идущих не обязательно по
линиям сетки) заведомо можно покрыть все эти узлы?
Покажем, что прямой покрыть узлы можно. Проекция салфетки на ось
— это отрезок, по длине не провосходящий диагонали
салфетки, то есть
Рассмотрим вертикальные линии сетки, пересекающие проекцию салфетки. Таких прямых не больше,
чем
Если их оказалось
или меньше , цель достигнуты. Если же их ровно
то самая левая и
самая правая из них содержат ровно по одному узлу, накрытому салфеткой, этот факт доказан в лемме ниже. Заменим
эти две прямые на одну прямую, проходящую через упомянутые узлы. В результате все нужные точки покрыты
прямой.
_________________________________________________________________________________________________________________________________________________________________________________
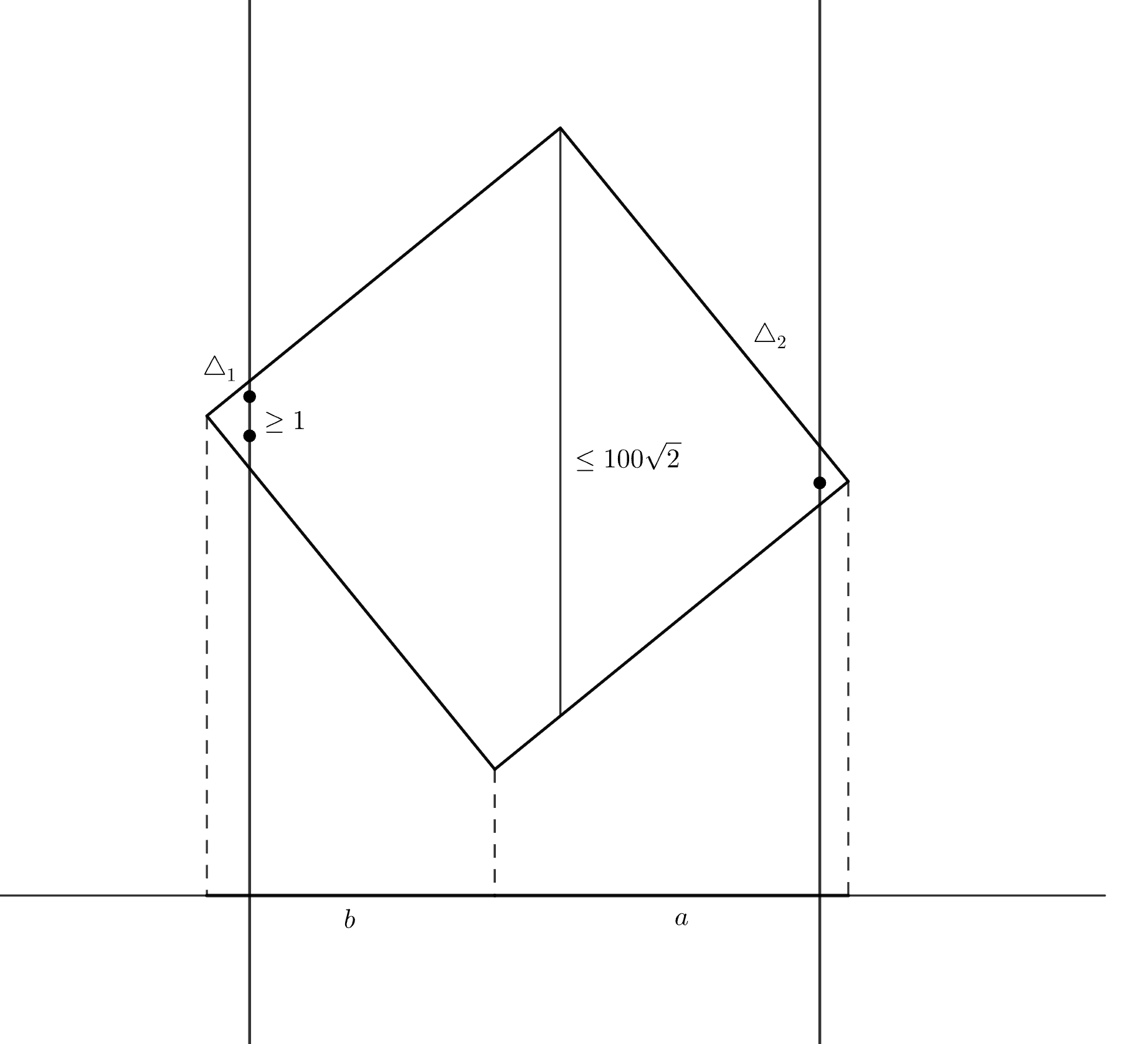
Лемма. Если салфетку пересекают вертикальные прямые, то самая левая и самая правая из них содержат ровно по одному узлу,
накрытому салфеткой.
Доказательство. Действительно, пусть проекции двух смежных сторон салфетки на горизонтальную прямую равны и
Допустим, что на одной из крайних прямых оказалось два или более узла. Тогда эта прямая отсекает от салфетки прямоугольный
треугольник
с гипотенузой, не меньше
Высота этого треугольника не превосходит
Треугольник
подобен треугольнику
который отсекает от салфетки прямая, проходящая через одну из вершин квадрата –
верхнюю или нижнюю в зависимости от того, у какой из них проекция правее. Гипотенуза этого треугольника не превосходит
диагонали квадрата, то есть
а высота равна
и
и значит, не меньше
Нам известно, что
Тогда
т.е. и
Записывая пропорциональность высот и гипотенуз в подобных треугольниках
и
получаем
С другой стороны,
— противоречие.
_________________________________________________________________________________________________________________________________________________________________________________
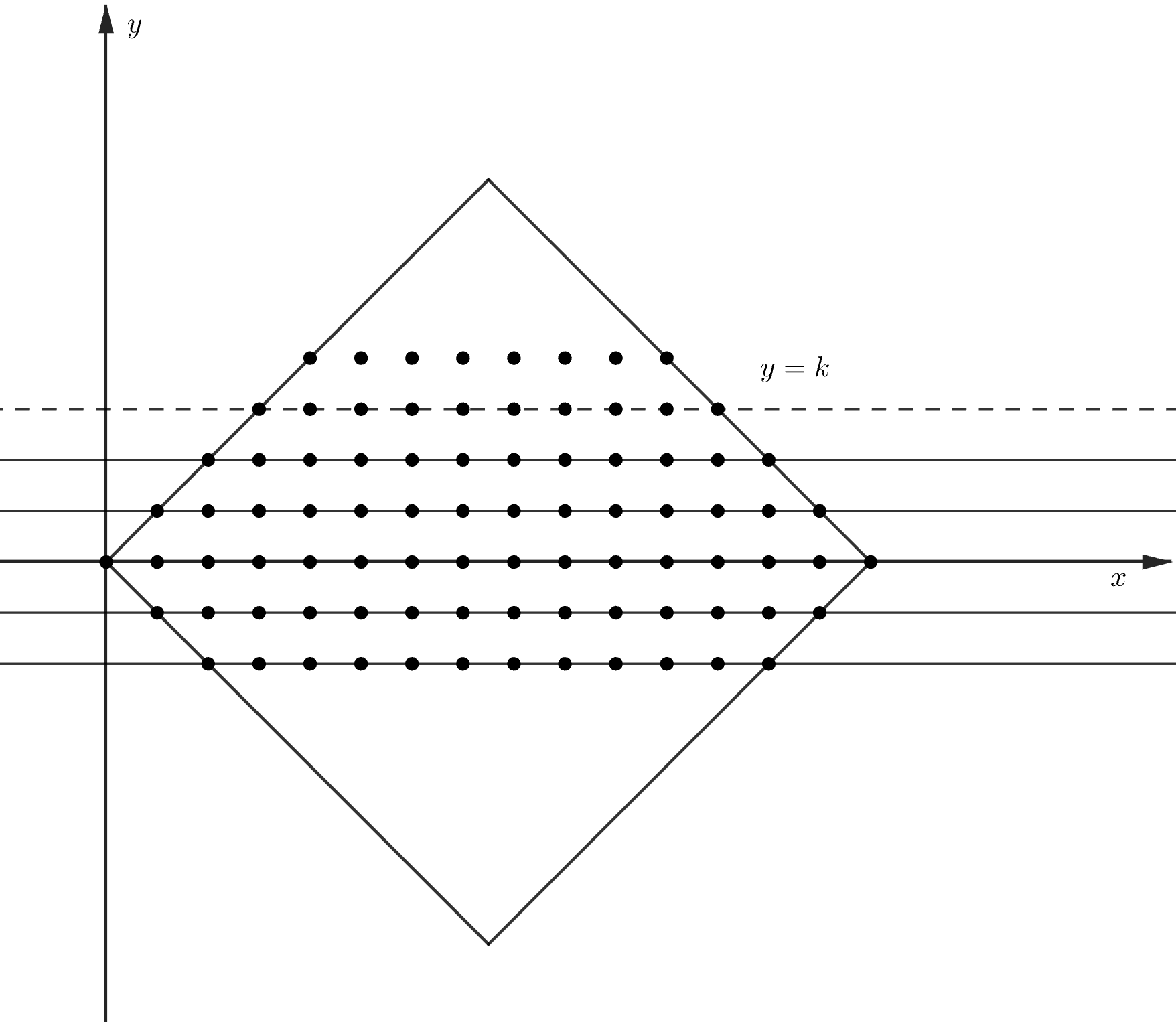
Докажем теперь, что не всегда возможно провести прямых так, чтобы они проходили через все узлы. Построим контрпример.
Возьмём координатную плоскость и расположим квадрат, диагональ которого расположена на оси
от точки
до
Его
сторона равна
поэтому его можно накрыть салфеткой со стороной
Проверим, что узлы, принадлежащие
квадрату, нельзя покрыть
прямыми. На диагонали расположено
узла. Если диагональ не лежит ни на одной из
проведённых прямых, то эти узлы должны покрываться различными прямыми, что невозможно, поскольку прямых всего
Поэтому прямая
обязательно проведена. Теперь докажем по индукции, что при
проведены прямые
База
уже проверена. Установим переход от
к
По предположению индукции уже проведены
прямые
(всего прямая). Рассмотрим очередную прямую
на ней лежит
узлов(на каждом шаге их количество
уменьшается на 2). Если она не проведена, то эти узлы покрыты различными прямыми, что невозможно, поскольку нам осталось
провести
прямых. Значит, она проведена. Аналогично должна быть проведена и прямая
Итак мы установили, что заведомо проведено
прямых. Но при этом точки
и
всё
ещё остались непокрытыми. Они являются вершинами прямоугольника и поэтому не могут быть покрыты одной прямой.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




