8.09 Первообразная и площадь под кривой
Ошибка.
Попробуйте повторить позже
— одна из первообразных функции
Найдите
По определению первообразной Тогда
откуда
Ошибка.
Попробуйте повторить позже
На рисунке изображён график функции — одной из первообразных некоторой функции
определённой
на интервале
Определите по рисунку количество решений уравнения
на отрезке
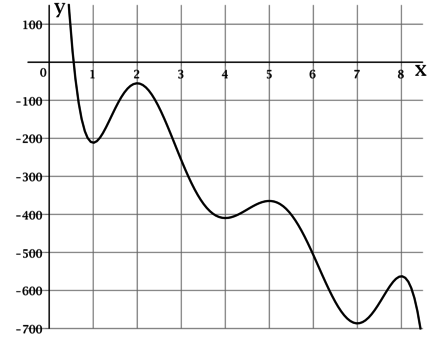
По определению первообразной тогда уравнение
равносильно
Производная функции равна 0 в
точности в тех точках, где касательная к графику функции параллельна оси
По рисунку видно, что на отрезке касательная к графику
параллельна оси
в точках с абсциссами
и
Таких точек две.
Ошибка.
Попробуйте повторить позже
На рисунке изображён график функции — одной из первообразных некоторой функции
определённой
на интервале
Определите по рисунку количество решений уравнения
на отрезке
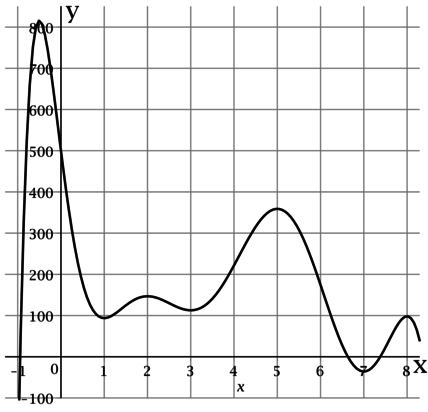
По определению первообразной тогда уравнение
равносильно
Производная функции равна 0 в
точности в тех точках, где касательная к графику функции параллельна оси
По рисунку видно, что на отрезке касательная к графику
параллельна оси
в точках с абсциссами
Таких точек пять.
Ошибка.
Попробуйте повторить позже
Известно, что — одна из первообразных функции
Найдите
По определению первообразной Тогда имеем:
Отсюда получаем
Ошибка.
Попробуйте повторить позже
Известно, что — одна из первообразных функции
Найдите
По определению первообразной Тогда имеем:
Отсюда получаем
Ошибка.
Попробуйте повторить позже
На рисунке изображён график функции — одной из первообразных
некоторой функции
определённой на интервале
Определите
по рисунку количество решений уравнения
на отрезке
По определению первообразной тогда уравнение
равносильно
Производная функции равна 0 в
точности в тех точках, где касательная к графику функции параллельна оси
По рисунку видно, что на отрезке касательная к графику
параллельна оси
в точках с абсциссами
Таких точек четыре.
Ошибка.
Попробуйте повторить позже
На рисунке изображён график функции — одной из первообразных некоторой функции
определённой на
интервале
Пользуясь рисунком, определите количество решений уравнения
на отрезке
![]()
Так как — одна из первообразных функции
то
Производная равна нулю в точках, в которых касательная к графику функции
расположена горизонтально.
Таких точек на отрезке
ровно 6.
![]()
Ошибка.
Попробуйте повторить позже
На рисунке изображён график функции Вычислите по рисунку
где
— одна из первообразных
функции
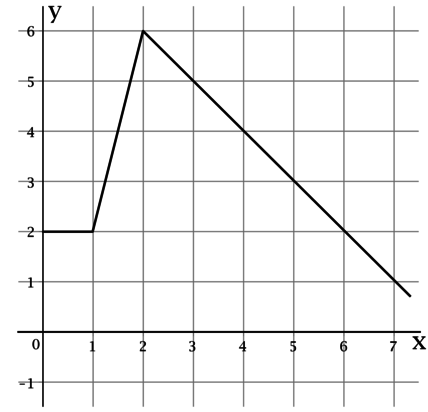
Площадь под графиком неотрицательной функции от точки
до точки
равна
где
— одна из
первообразных функции
Рассмотрим выражение
Это взятая с минусом площадь под графиком от точки
до точки
Площадь под графиком от точки
до точки
равна 6, тогда
Ошибка.
Попробуйте повторить позже
На рисунке изображён график функции Функция
— одна из первообразных функции
Найдите площадь закрашенной фигуры.
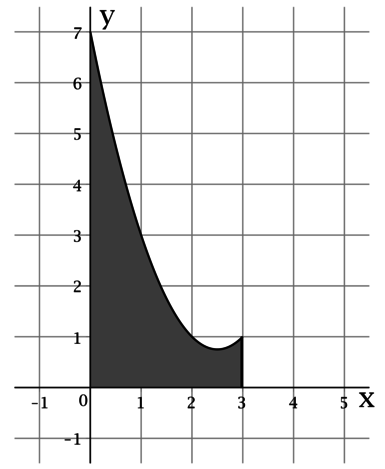
Площадь под графиком неотрицательной функции от точки
до точки
равна
где
— одна из первообразных функции
Таким образом, площадь закрашенной фигуры равна
Ошибка.
Попробуйте повторить позже
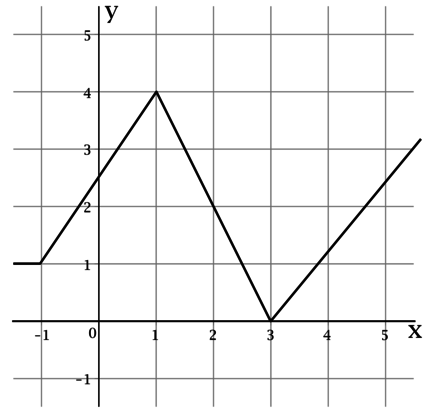
На рисунке изображён график функции Вычислите по рисунку
где
— одна из первообразных
функции
Площадь под графиком неотрицательной функции от точки
до точки
равна
где
— одна из
первообразных функции
Таким образом, — площадь под графиком
от точки
до точки
Площадь под графиком от точки
до точки
равна сумме площадей прямоугольной трапеции и
прямоугольного треугольника.
Тогда имеем:
Ошибка.
Попробуйте повторить позже
На рисунке изображён график функции Функция
— одна из первообразных функции
Найдите площадь закрашенной фигуры.
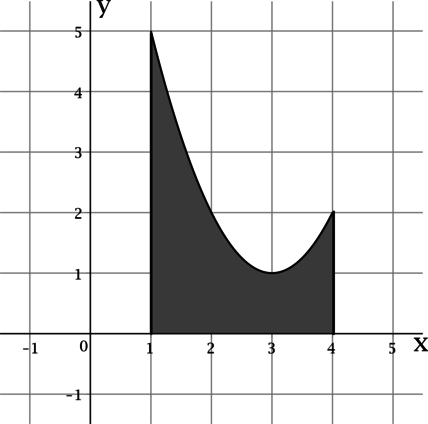
Площадь под графиком неотрицательной функции от точки
до точки
равна
где
— одна из
первообразных функции
Таким образом, площадь закрашенной фигуры равна
Ошибка.
Попробуйте повторить позже
На рисунке изображён график функции Пользуясь рисунком, вычислите
где
— одна из
первообразных функции
![]()
По формуле Ньютона-Лейбница имеем:
Заметим, что такой интеграл равен площади под графиком функции на отрезке
Значит, нам
нужно найти площадь выделенной фигуры, состоящей из прямоугольного треугольника и двух прямоугольников:
![]()
Тогда имеем:
Ошибка.
Попробуйте повторить позже
На рисунке изображён график некоторой функции Функция
— одна из первообразных функции
Найдите
площадь закрашенной фигуры.
Нам нужно найти площади под графиком функции на отрезке
Такая площадь равна интегралу
По
формуле Ньютона-Лейбница имеем:
Ошибка.
Попробуйте повторить позже
На рисунке изображён график функции — одной из первообразных
функции
определённой на интервале
Найдите количество решений
уравнения
на отрезке
По определение первообразной то есть решением уравнения
будут точки экстремума функции
которые помечены на графике.
Получим семь точек.



