Окружность Аполлония
Ошибка.
Попробуйте повторить позже
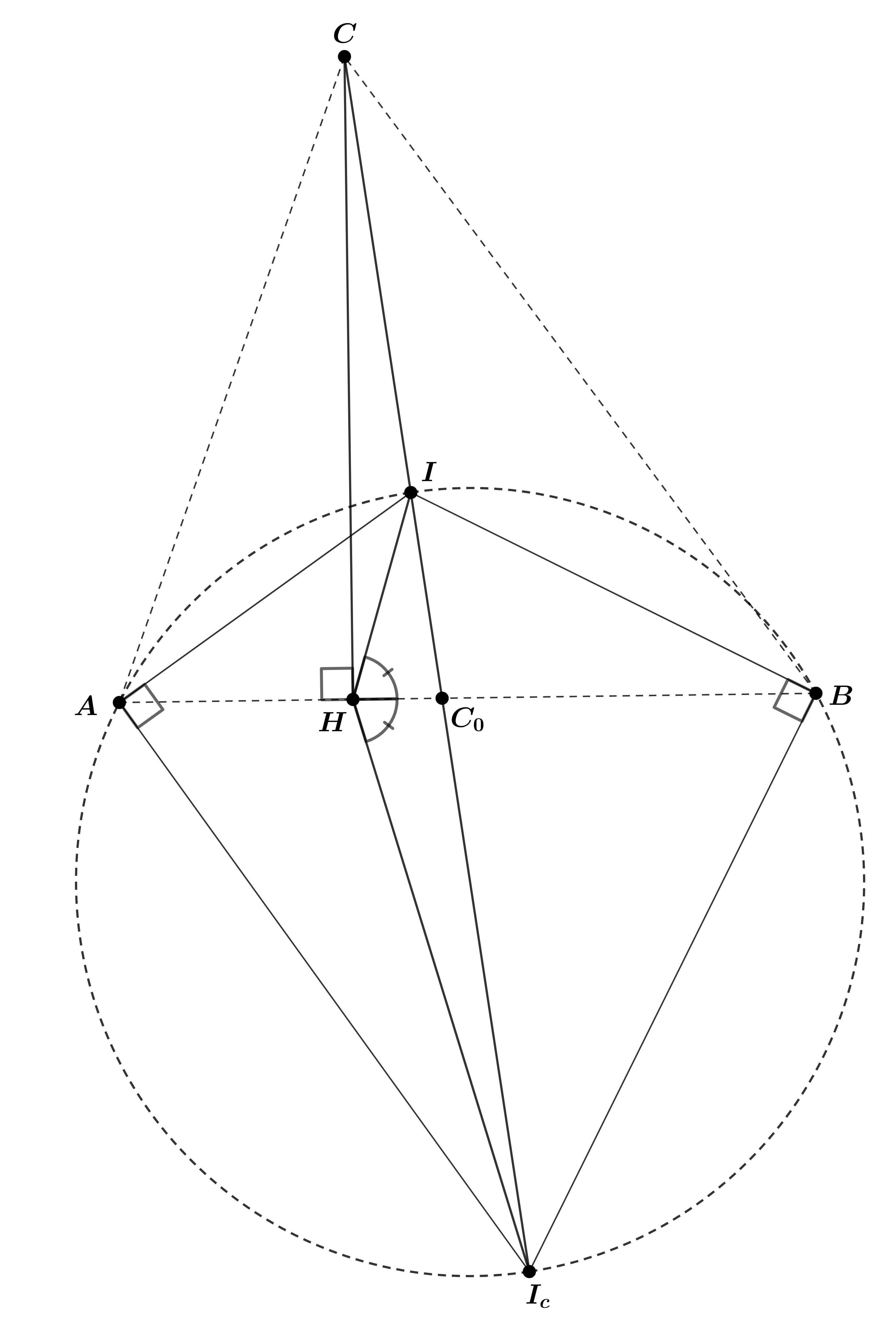
В треугольнике отметили центр вписанной окружности, основание высоты, опущенной на сторону
и центр вневписанной
окружности, касающейся этой стороны и продолжений двух других. После этого сам треугольник стёрли. Восстановите его с помощью
циркуля и линейки.
Подсказка 1
Обозначим за I и I_c центр вписанной и вневписанной окружности соответственно. Пусть C₀ — основание биссектрисы угла C. Давайте попробуем что-то сказать про отношение CI/CI_c.
Подсказка 2
Попробуйте выразить его через радиус вписанной окружности и вневписанной (далее будем обозначать их r и r_c соответственно).
Подсказка 3
CI/CI_c = r/r_c в силу теоремы Фалеса. Какое еще отношение равно этим двум, учитывая, что расстояния от точек I и I_c до стороны AB также равно r и r_c соответственно?
Подсказка 4
Правильно! CI/CI_c = r/r_c = IC₀/I_cC₀! Что же тогда можно сказать про окружность с диметром CC₀?
Подсказка 5
Верно! Она является окружностью Аполлония для точек I и I_c. Теперь вспомним про основание высоты. Обозначим его за H. Что можно сказать про прямую HC₀ и HC кроме того, что они перпендикулярны?)
Подсказка 6
Ага! H лежит на окружности с диаметром CC₀, а значит, эти прямые являются биссектрисой и внешней биссектрисой угла IHI_c соответственно! Теперь совсем понятно, как восстановить точку C и сторону AB, но как восстановить сами точки A и B?
Подсказка 7
Для этого вспомните, чему равны углы IBI_c и IAI_c?
Центры вписанной и вневписанной окружностей и
лежат на биссектрисе угла
Пусть
— точка пересечения этой биссектрисы
со стороной
Тогда
где
— радиусы вписанной и вневписанной окружностей. Поэтому для любой
точки
окружности с диаметром
отношение
будет одним и тем же. Так как основание
высоты, опущенной на
лежит на этой окружности,
т.е. и
— внутренняя и внешняя биссектрисы угла
Следовательно, проведя эти биссектрисы, мы восстановим точку
и прямую
Поскольку
точки
лежат на окружности с диаметром
Соответственно, построив эту
окружность и найдя точки ее пересечения с прямой
мы восстановим треугольник.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




