Окружность Аполлония
Ошибка.
Попробуйте повторить позже
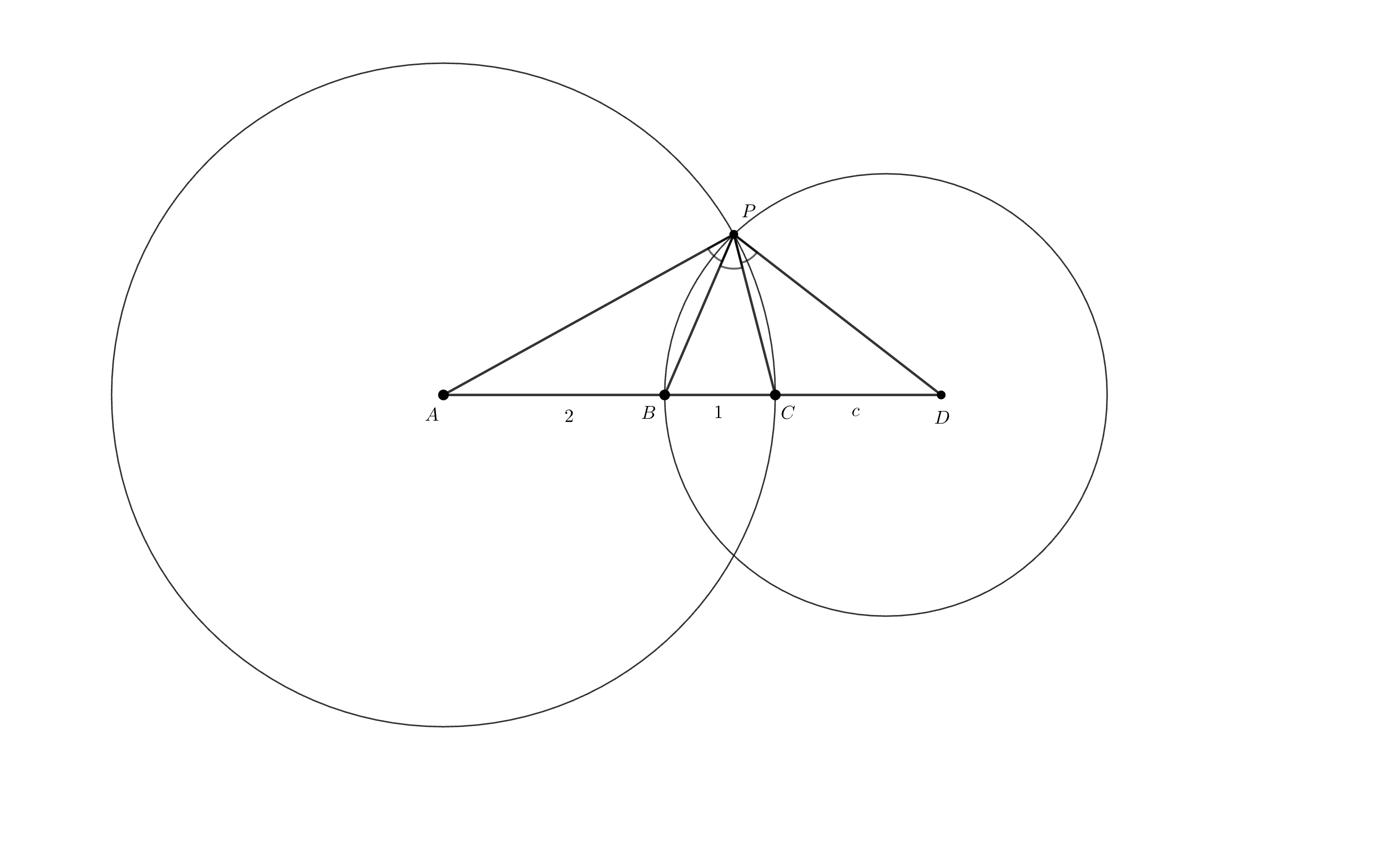
Точки расположены на прямой в указанном порядке, причем
Найдите все положительные
для
каждого из которых найдется такая точка
(не лежащая на прямой
), что
— трисектрисы (лучи, делящие угол на три
равные части) угла
Источники:
Подсказка 1
Попробуйте подумать о конструкции, называемой окружностью Аполлония. Пусть A и B — фиксированные точки, k ≠ 1. Хотим найти все точки X такие, что AX/BX = k. Зададим систему координат, в которой A = (-a;0), B = (a;0), где a = AB/2. Пусть X = (x;y), тогда AX²/BX² = k² = ((x + a)² + y²) / ((x - a)² + y²). Получим уравнение (x + a ⋅ (k²+1) / (k²-1))² + y² = (2ka / (k² - 1))², которое и называют окружностью Аполлония, ее радиус равен k ⋅ AB / |k² - 1|.
Подсказка 2
Можно заметить, про при k > 1 точка A будет находиться вне окружности, а точка B — внутри.
Подсказка 3
Пусть окружность Аполлония для отрезка AB пересекает его в точке С, докажите, что для любой точки P, лежащей на окружности, PC будет биссектрисой ∠APB.
Подсказка 4
Рассмотрите окружности Аполлония для точек A, C и B, D.
Подсказка 5
Окажется, что окружности должны иметь 2 общих точки! Какие могут быть c?
Сначала рассмотрим вспомогательную конструкцию: пусть для фиксированных точек AB и фиксированного положительного
требуется найти все точки
плоскости, для которых
Зададим систему координат, в которой
и
для
Тогда
Отсюда:
Это уравнение окружности, называемой окружностью Аполлония точек
и ее радиус равен
Заметим, что для
точка
находится вне этой окружности, а точка
–– внутри нее.
_________________________________________________________________________________________________________________________________________________________________________________
Лемма. Если — окружность Аполлония точек
и
пересекает отрезок
в точке
то для любой точки
выполнено
т.е.
— биссектриса угла
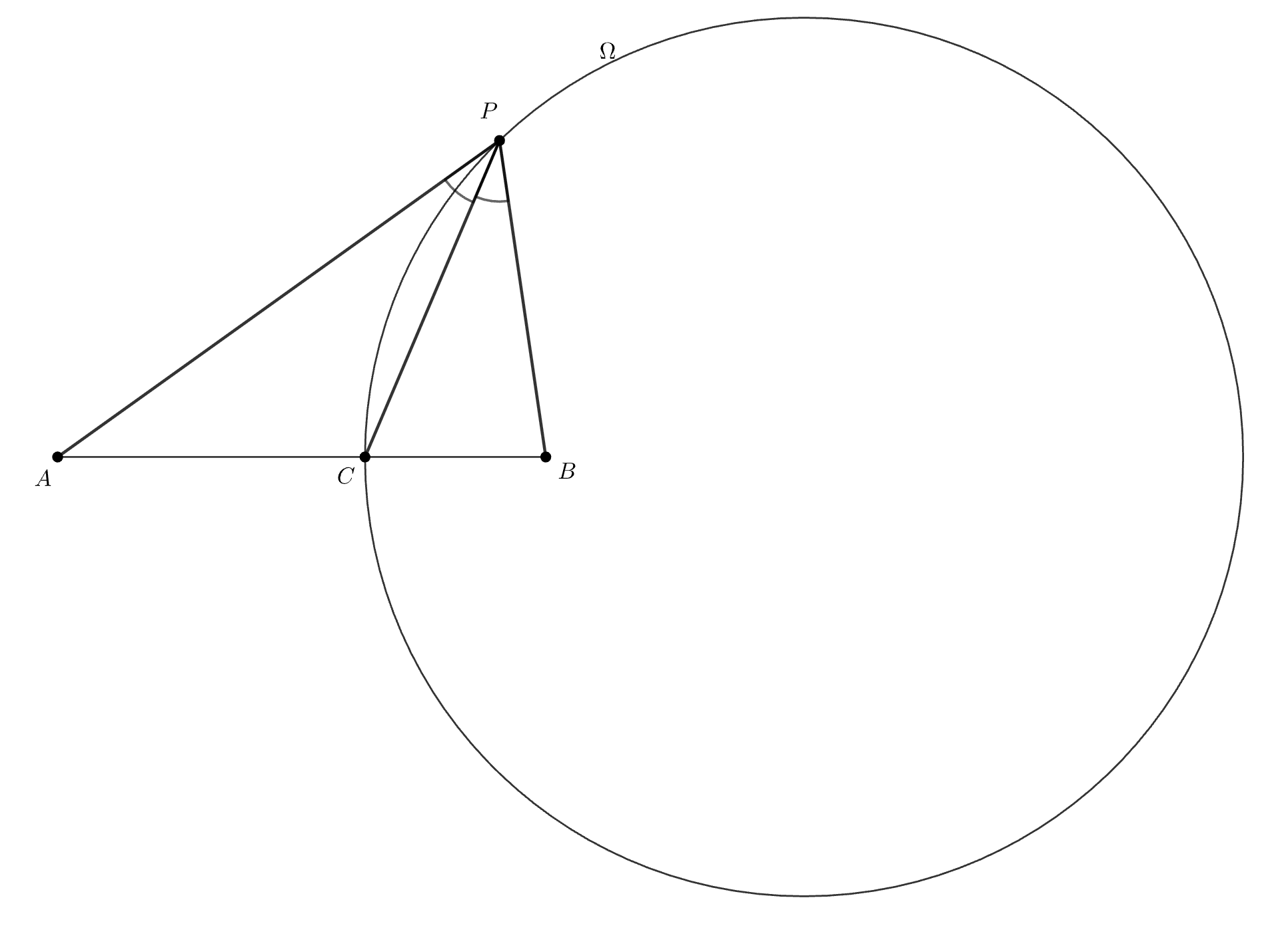
Заметим, что точка лежит на
значит, по геометрическому месту точек для окружности Аполлония
Следовательно, по обратной теореме о биссектриcе — бассектриса угла
______________________________________________________________________________________________________________________________________________________
Вернемся к задаче. Ввиду доказанного выше, необходимо, чтобы окружности Аполлония для и
имели две общие точки (поскольку центры окружностей лежат на прямой
единственная общая точка этих
окружностей лежала бы на этой же прямой). Ясно, что если
то точка
лежит внутри второй окружности, тогда две окружности
пересекаются. Если
то точка
лежит на срединном перпендикуляре к
который пересекает первую окружность ввиду
Если же то для пересечения окружностей необходимо и достаточно
откуда ввиду
получим
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




