Окружность Аполлония
Ошибка.
Попробуйте повторить позже
Пусть 
— описанная окружность неравнобедренного треугольника 
Пусть 
— окружность Аполлония, определённая точками 
и 
и проходящая через вершину 
Пересекающиеся окружности называются ортогональными, если касательные к ним в точке
пересечения перпендикулярны. Докажите, что 
и 
ортогональны.
Пусть 
и 
— основания внутренней и внешней биссектрис угла 
Как известно, 
— это окружность, описанная около
треугольника 
Следовательно, по теореме об угле между хордой и касательной касательная в точке 
к 
— прямая,
составляющая с 
угол, равный 
а касательная к 
в точке 
— прямая, составляющая с 
угол, равный
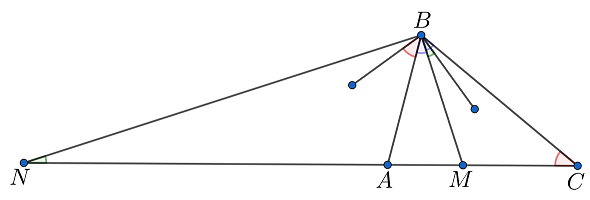
Таким образом, нам нужно доказать, что
Заметим, что
потому что это внешний угол у треугольника 
Угол 
— прямой, потому что биссектрисы смежных углов перпендикулярны,
а значит,
Специальные программы
Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!
Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.
Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.
Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».
Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!
Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!
