Окружность Аполлония
Ошибка.
Попробуйте повторить позже
Пусть — окружность Аполлония, определённая точками
и
и проходящая через вершину
Аналогично определим
окружности
и
Пусть точка
— одна из точек пересечения окружностей Аполлония
и
— лежит внутри
треугольника
. Докажите, что проекции точки
на стороны треугольника
являются вершинами равностороннего
треугольника.
Подсказка 1
Давайте опустим перпендикуляры и посмотрим, что за фигура получается. Это вписанный четырёхугольник. Также раз нас просят доказать, что треугольник равносторонний, в этой задаче, скорее всего, проще сделать это через равенство сторон, то есть отрезки. Какую теорему тогда хорошо бы применить в связи с вписанностью? Конечно с участием интересующего нас отрезка.
Подсказка 2
Верно, можно два раза применить теорему синусов, для треугольника ABC и окружности, образованной перпендикулярами. То есть глобально нам нужно хорошо выразить P_a P_c через другие отрезки. В итоге получим, что P_a P_c = BP*AC/(2R). Для других отрезков считается аналогично. Отлично, давайте теперь вернёмся к условию. Какое условие мы ещё забыли применить в задаче? Что означает пересечение трёх окружностей в точке P?
Подсказка 3
Ага, точка P лежит на трёх окружностях Аполлония. Но ещё проходит через одну из вершин треугольника. Тогда можно записать равенство отношений. А теперь, возвращаясь к основной идее, подумайте, как можно преобразовать это равенство, чтобы получились наши отрезки. Тогда и они будут равны, победа!
Обозначим эти проекции в соответствии с вершинами, напротив которых лежат эти точки.
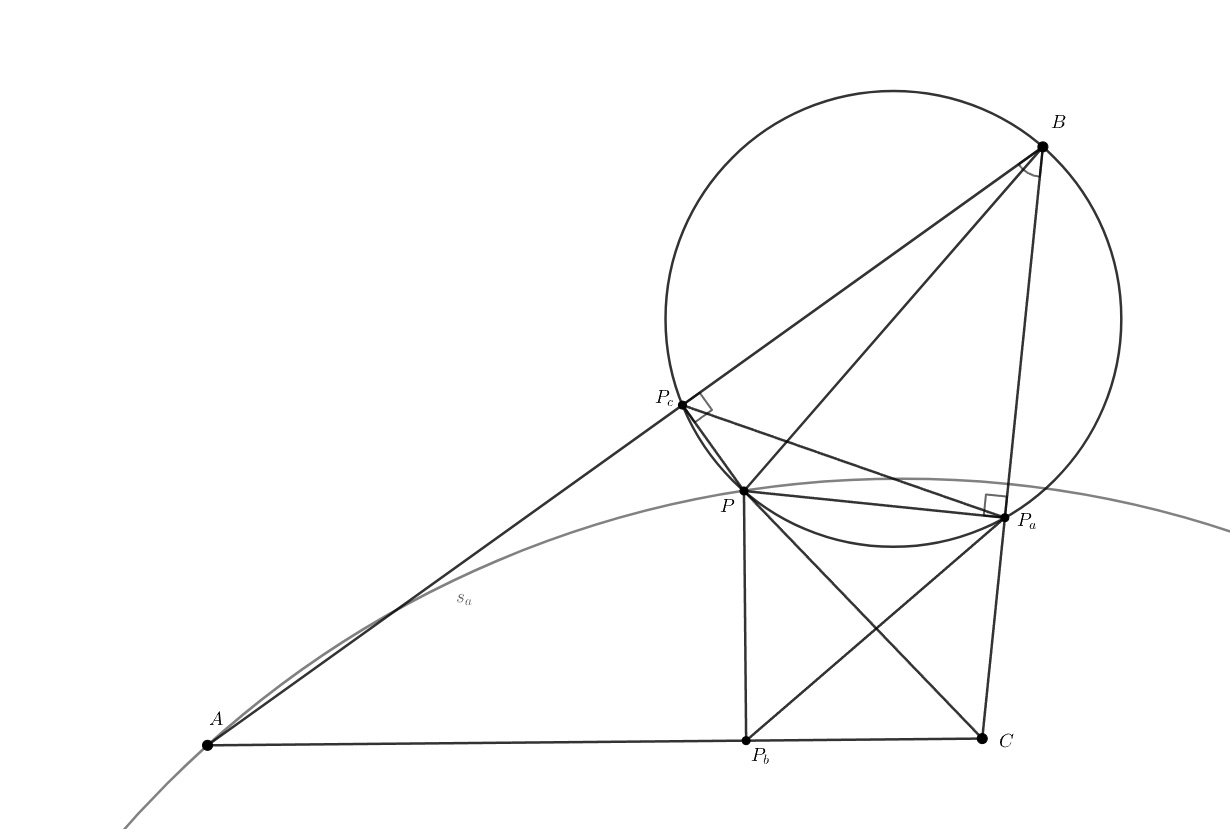
Из противоположных прямых углов в становится ясно, что он вписанный. После двукратного применения теоремы
синусов
где — радиус описанной окружности
Аналогично получаются формулы для двух других сторон педального треугольника:
По условию нашей задачи а тогда
Аналогично доказывается равенство
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




