Стереометрия на Энергетике
Ошибка.
Попробуйте повторить позже
Две сферы касаются друг друга внешним образом и каждая из них касается внутренним образом большей сферы. Радиус одной в два
раза, а другой — в три раза меньше радиуса наибольшей сферы. В точке касания малых сфер друг с другом построена
касательная плоскость к ним. Найдите расстояние от этой плоскости до центра наибольшей сферы, если ее радиус равен
Источники:
Проведём сечение описанной композиции плоскостью, проходящей через центры трех сфер. Искомое расстояние будет длиной отрезка 
на этой плоскости.
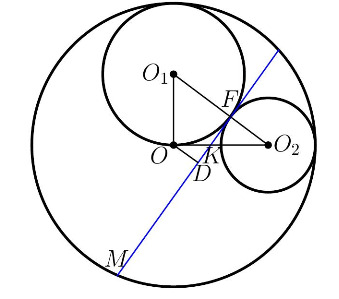
Пусть радиусы малых окружностей равны 
и 
Тогда радиус наибольшей (внешней) равен 
(дано: 
). Рассмотрим
Его стороны равны 
и 
следовательно, он прямоугольный.
Обозначим точку пересечения искомой хорды с отрезком 
через 
а с отрезком 
через 
Опустим из центра наибольшей
окружности перпендикуляр 
на искомую хорду (отрезок общей касательной). Тогда искомая хорда делится точкой 
пополам и
перпендикулярна отрезкам 
и 
Прямоугольные треугольники 
подобны. Поэтому 
, откуда 
и 
Далее, 
откуда 
Специальные программы
Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!
Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.
Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.
Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».
Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!
Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!
