Комбинаторика на Изумруде: клетчатые задачи, игры, способы, процессы
Ошибка.
Попробуйте повторить позже
В каждую клетку шахматной доски 
записали некоторое натуральное число, не превосходящее 
Сказочная шахматная фигура
кузнечик стоит в одной из угловых клеток. Каждым своим ходом кузнечик может прыгнуть в клетку, стоящую в той
же горизонтали или вертикали, что и кузнечик, и отстоящую от кузнечика на столько клеток, какое число записано в
клетке с кузнечиком (в частности, если в клетке с кузнечиком записано число 
он может переместиться на одну из
соседних с ним по горизонтали или по вертикали клеток). Известно, что за 
прыжка кузнечик может посетить все
клетки доски, побывав в каждой ровно один раз. Какое наибольшее количество троек могло быть написано в клетках
доски?
Источники:
Разобьём клетки доски на группы, как показано на рисунке 
(разными цифрами обозначены разные группы). Заметим, что если в
какой-либо группе клеток все написанные числа равны трём, то кузнечик, прыгая по клеткам этой группы, никогда не сможет попасть в
клетки другой группы. Так как кузнечик может обойти все клетки доски, он смог переместиться между клетками разных групп хотя бы 
раз. Значит троек могло быть не более 
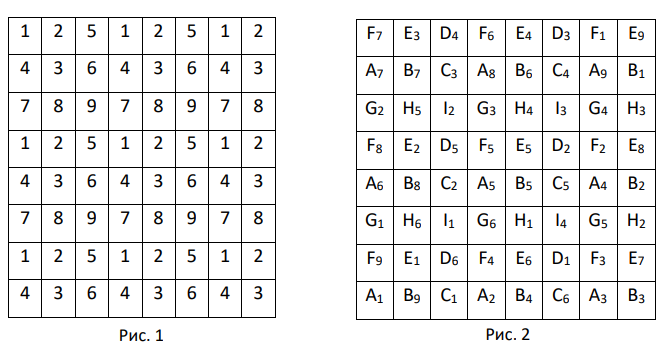
Приведём пример заполнения клеток таблицы и порядка обхода этих клеток кузнечиком (см. рисунок 
В клетках
стоят единицы, во всех остальных — тройки. Порядок обхода 
по
возрастанию индексов.
Специальные программы
Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!
Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.
Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.
Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».
Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!
Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!
