Комбинаторика на Изумруде: клетчатые задачи, игры, способы, процессы
Ошибка.
Попробуйте повторить позже
На доске размером стоит сказочная шахматная фигура принцесса. За один ход принцесса может передвинуться либо на одну
клетку вправо, либо на одну клетку вверх, либо на одну клетку по диагонали влево-вниз. Какое наибольшее число не бьющих друг друга
принцесс можно поставить на доску?
Источники:
Подсказка 1
В задачах на оценку объектов на доске очень часто помогает идея разбить доску на кусочки поменьше, в которых мы точно может оценить количество объектов. На какие кусочки будем делить? ;)
Подсказка 2
Попробуйте оценить количество принцесс в прямоугольнике 2 на 3.
Подсказка 3
Попробуйте разместить в прямоугольнике 2 на 3 3 принцессы ;)
Подсказка 4
Именно, оказывается, что на доске 2 на 3 стоит не больше двух принцесс! Отсюда можно сделать оценку на их количество для всех доски) Не забудьте придумать пример!
Заметим, что в прямоугольниках и
находится не больше одной принцессы. Иначе в прямоугольнике
левая принцесса
била бы правую, а в прямоугольнике
нижняя принцесса — верхнюю. Значит, принцессы не могут быть в соседних по стороне
клетках.
Покажем, что в прямоугольнике не более двух принцесс. Предположим, что в таком прямоугольнике можно разместить хотя бы
фигуры принцесс. Так как принцессы не являются соседями по стороне, то возможны два варианта их размещения (розовые квадратики
— фигуры прицесс)
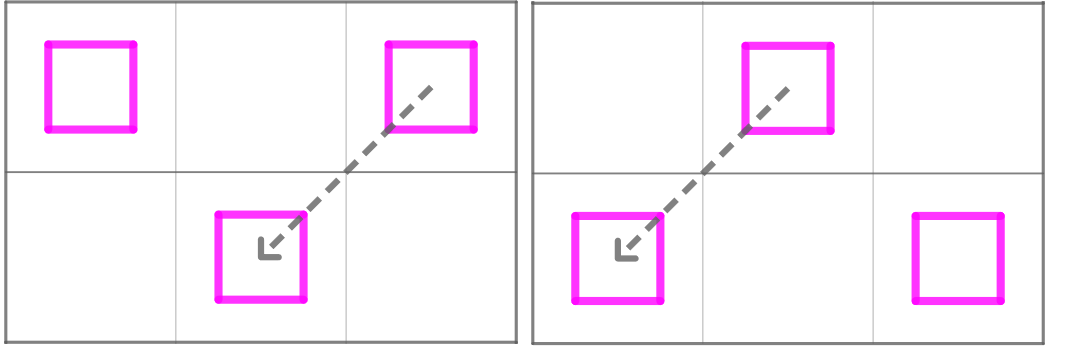
В обоих случаях найдется принцесса, которая будет побита.
Тогда если разбить доску на
непересекающиеся области размера
получим, что принцесс не более
48 принцесс разместить уже возможно:
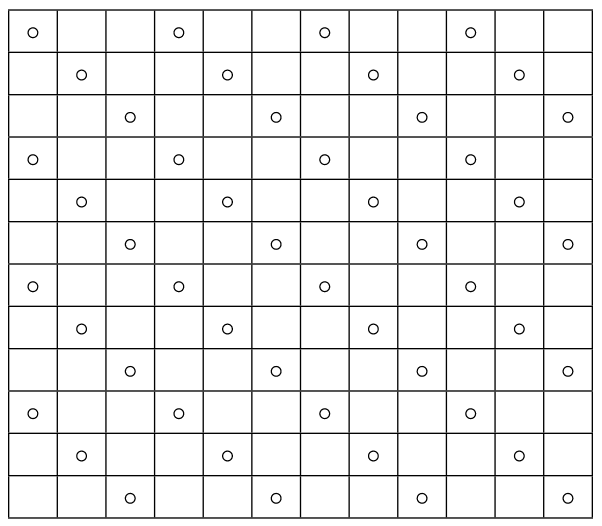
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




