ГМТ, расположение объектов на плоскости

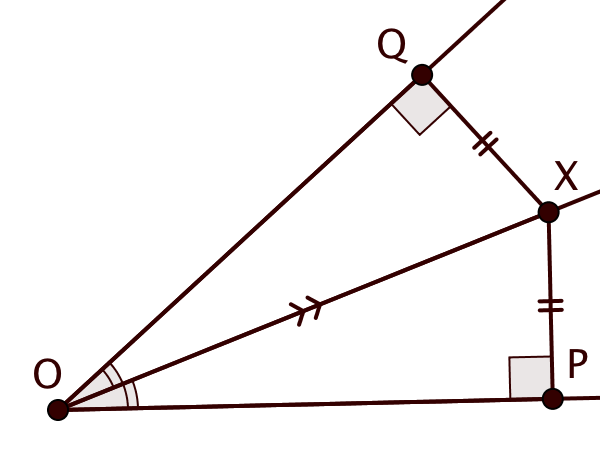
Сначала докажем, что любая точка биссектрисы обладает указанным свойством. Обозначим вершину угла через а произвольную точку на биссектрисе через Опустим из перпендикуляры и на стороны угла. Так как  — биссектриса то Поэтому, у прямоугольных треугольников и равны углы и общая гипотенуза. Значит, В равных треугольниках соответствующие элементы равны, значит, Таким образом, расстояния от произвольной точки до сторон угла равны, значит, все точки биссектрисы равноудалены от сторон угла.

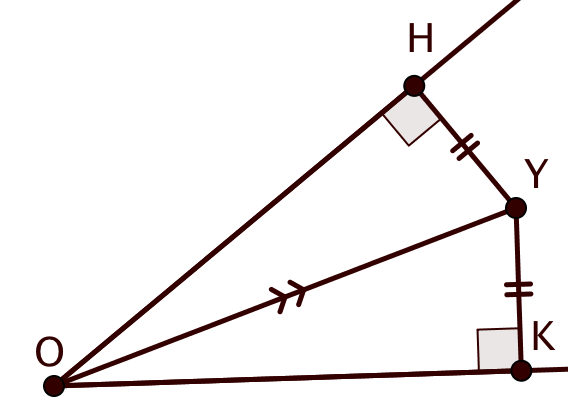
Теперь докажем, что любая точка, обладающая указанным свойством, лежит на биссектрисе. Рассмотрим произвольную точку равноудаленную от сторон угла. Опустим из нее на стороны угла перпендикуляры и Из равноудаленности следует, что отрезки Поэтому прямоугольные треугольники и равны по общей гипотенузе и равным катетам. Значит, соответствующие то есть точка лежит на биссектрисе.

Обратите особое внимание на доказательство в обе стороны: мы доказываем как то, что любая точка биссектрисы равноудалена от сторон углов, так и то, что любая точка, равноудаленная от сторон угла, лежит на биссектрисе.

Доказательства лишь в одну сторону недостаточно: может так получиться, что, например, не все точки, подходящие под заданное условие, принадлежат указанному геометрическому месту. Например, множество точек, равноудаленных от двух данных прямых (кроме внутренней биссектрисы в этом случае еще подходит внешняя биссектриса), или множество точек для данных точек и таких, что треугольник  — прямоугольный (кроме окружности, построенной на как на диаметре, если мы не уточняем, какой именно угол прямой, также подходят две перпендикулярные отрезку прямые, проходящие через и через соответственно, более того, сами точки и надо «выколоть»).