ГМТ, расположение объектов на плоскости
Ошибка.
Попробуйте повторить позже
В четырёхугольнике
— середина
— середина
Серединные перпендикуляры к
и
пересекаются в точке
Докажите, что
лежит на серединном перпендикуляре к отрезку
Подсказка 1
То, что точка лежит на серединном перпендикуляре к отрезку, означает, что она равноудалена от концов этого отрезка. Соедините точку Р с вершинами четырехугольника и найдите равные отрезки.
Подсказка 2
PB = PA и PC = PD. Что тогда можно сказать про треугольники PBC и PAD?
Подсказка 3
Они равны! Теперь рассмотрите на отрезки PN и PM.
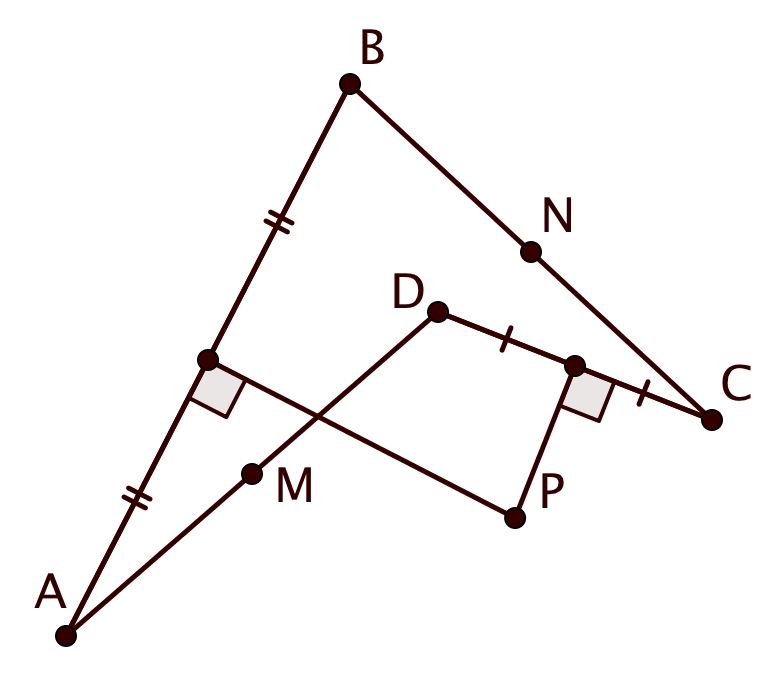
Так как точка лежит на серединном перпендикуляре к
то
Аналогично, так как точка
лежит на серединном
перпендикуляре к
выполнено
Кроме того, по условию
Поэтому
по трем
сторонам.
Заметим, что и
— медианы этих треугольников, проведенные к равным сторонам
и
В равных треугольниках
соответствующие элементы равны, то есть
Это и означает, что лежит на серединном перпендикуляре к
Замечание. Использование серединных перпендикуляров к отрезкам и
как ГМТ вместо привычного равенства треугольников
позволяет избавиться от рассмотрения различных случаев картинки. В приведенном решении как раз от расположения точки
ничего не
зависит.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




