ГМТ, расположение объектов на плоскости
Ошибка.
Попробуйте повторить позже
Найдите ГМТ середин хорд длины в данной окружности.
Подсказка 1
Возьмем хорду AB длиной d и ее середину — точку M. Можно ли выразить расстояние от центра окружности до точки M?
Подсказка 2
Конечно! Пусть O — центр окружности, R — ее радиус. Тогда по теореме Пифагора OM = √(R² - d²/4). Точкой какой известной фигуры тогда является M?
Подсказка 3
Конечно, это окружность с радиусом, который мы посчитали ранее и центром M. Но ГМТ — это множество. Мы доказали, что если M — середина хорды длиной d, то она лежит на этой окружности. Чего еще не хватает?
Подсказка 4
Правильно! Нужно еще доказать, что если точка лежит на этой окружности, то она является серединой хорды длиной d. Остается это проверить, и дело в шляпе!
Подсказка 5
Интуиция не должна нас подводить! Проводим касательную к окружности, которую предполагаем ответом, в любой точке. Тогда пересечение этой касательной и исходной окружности дают хорду. Осталось посчитать ее длину!
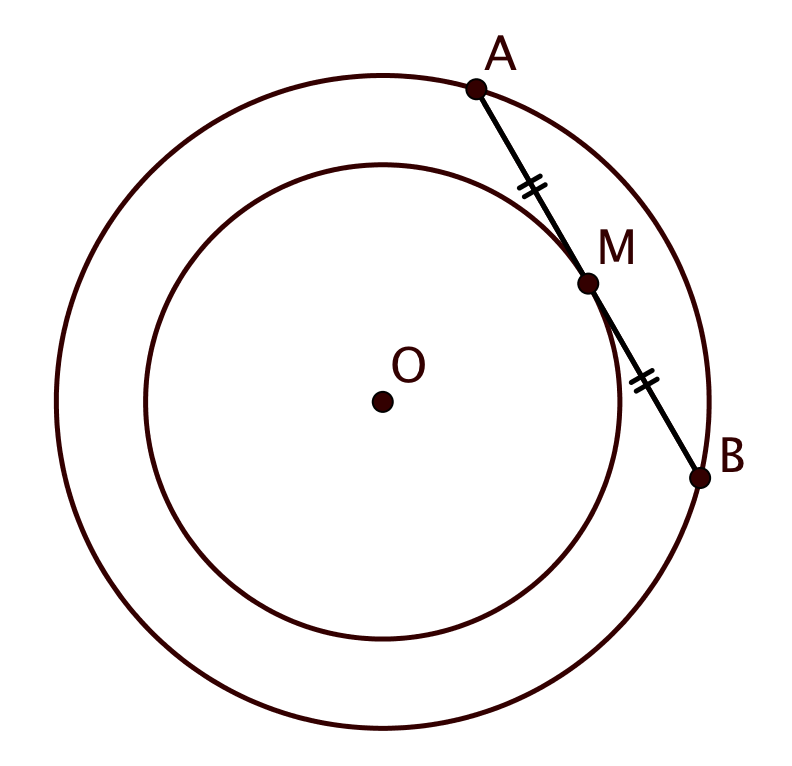
Рассмотрим произвольную точку удовлетворяющую условию, и обозначим отрезок длины
серединой которого она является, через
Тогда
как медиана равнобедренного
Поэтому по теореме Пифагора
значит, точка
лежит на указанной окружности.
В другую сторону, рассмотрим произвольную точку лежащую на окружности из ответа. Проведем к этой окружности касательную,
обозначим точки пересечения этой касательной с исходной окружностью через
и
Тогда
как радиус,
проведенный в точку касания. Поэтому
и
можно найти из теоремы Пифагора для прямоугольных
и
откуда
Значит,
и указанная точка
является серединой хорды
длины
Обозначим центр исходной окружности через и радиус через
. Тогда искомое ГМТ — окружность с центром
и радиусом
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




