ГМТ, расположение объектов на плоскости
Ошибка.
Попробуйте повторить позже
Дан треугольник Внутри него взяли точку
и соединили ее с вершинами. Получилось три треугольника. Найдите ГМТ
для
которых сумма площадей двух из этих треугольников будет равна площади третьего.
Подсказка 1
Рассмотрим одну такую точку М. Пусть S(BMC) = S(AMB) + S(AMC). Как тогда можно выразить площадь всего треугольника через площадь BMC?
Подсказка 2
Площадь ABC в два раза больше площади BMC! Заметим, что у этих треугольников общее основание. А как относятся друг к другу их высоты?
Подсказка 3
Из формулы площади через высоту и основание можно понять, что высота, проведённая к BC у треугольника BMC в 2 раза меньше соответствующей высоты у треугольника ABC. Тогда где находятся все такие точки М? Не забудьте рассмотреть аналогичные случаи, когда площади других треугольников равны сумме площадей оставшихся.
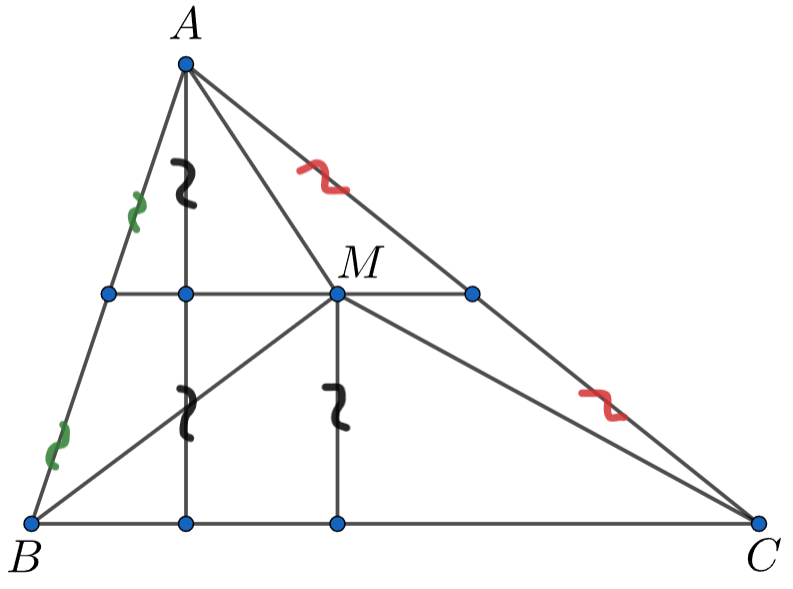
Пусть Но тогда
то есть
У треугольников
и
одинаковое основание
Значит, высота, проведённая к
у треугольника
в
раза меньше соответствующей высоты у
треугольника
Следовательно, все такие точки
находятся на расстоянии половины высоты треугольника
проведённой к
от прямой
Осталось заметить, что все такие точки находятся на средней линии, потому что она делит высоту треугольника
пополам и параллельна
серединный треугольник , то есть треугольник, образованный тремя средними линями
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




