ГМТ, расположение объектов на плоскости

(a) Как известно, серединный перпендикуляр — ГМТ, равноудаленных от концов отрезка. Обозначим середину отрезка через . Тогда совершенно очевидно, что для точек на луче расстояние до точки меньше, чем до , а для точек на луче  — наоборот, расстояние до точки больше, чем до .

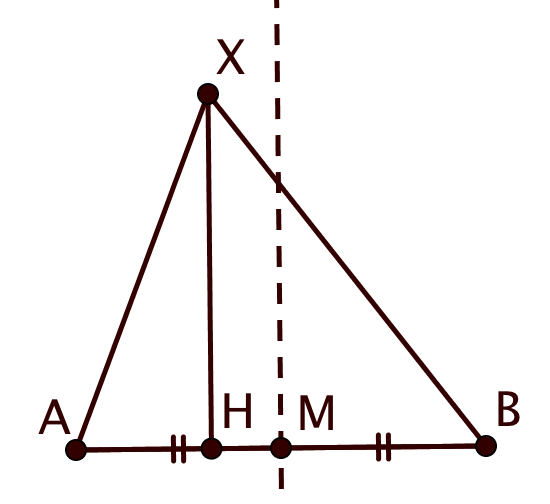
Теперь рассмотрим произвольную точку плоскости. Обозначим её проекцию на прямую через . Если точка лежит по одну сторону с точкой относительно серединного перпендикуляра, то и лежит на луче . Тогда , а по теореме Пифагора , или , то есть для любой точки, лежащей по одну сторону от серединного перпендикуляра с точкой , расстояние до меньше, чем до . Аналогично для точки, лежащей по одну сторону с относительно серединного перпендикуляра расстояние до меньше, чем до . Отсюда и ответ.

(b) Обозначим середины сторон , и через , и соответственно, а точку пересечения серединных перпендикуляров к сторонам треугольника через . Тогда искомое ГМТ — угол, образованный как пересечение двух полуплоскостей, ограниченных прямыми и . Полуплоскость, ограниченная прямой , включает точку , а полуплоскость, ограниченная прямой , включает точку .

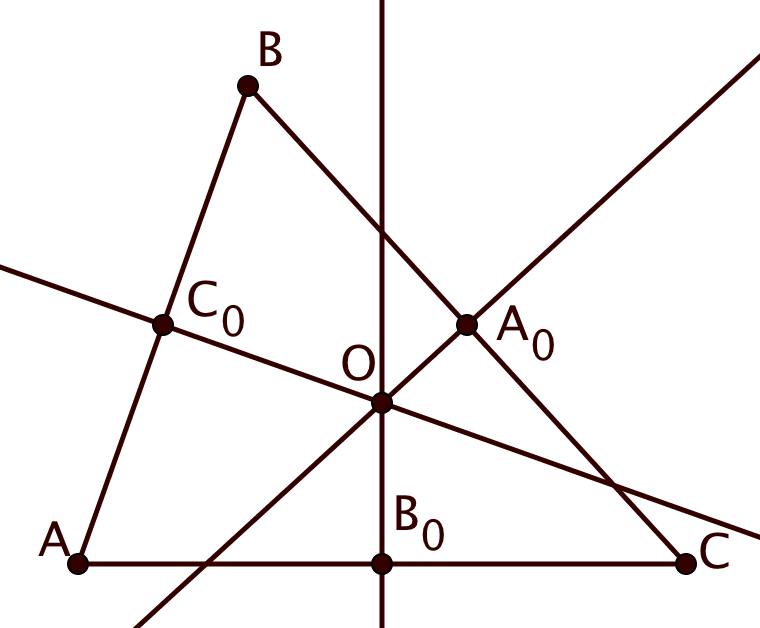
Как мы знаем по пункту (а), ГМТ , для которых , — полуплоскость, ограниченная прямой , содержащая точку . Также, ГМТ , для которых , — полуплоскость, ограниченная прямой , содержащая точку . Поэтому все точки , подходящие под условие , могут лежать только в пересечении этих двух полуплоскостей. Более того, если точка лежит в этом пересечении, то по тому же пункту (а), она удовлетворяет двум неравенствам и , поэтому двойное неравенство также верно.

(c) Обозначим середину через и проведем к серединный перпендикуляр. Так как , то по пункту (а) точка лежит по ту же сторону относительно этого серединного перпендикуляра, что и . Аналогично, точка также лежит относительно серединного перпендикуляра по ту же сторону, что и .

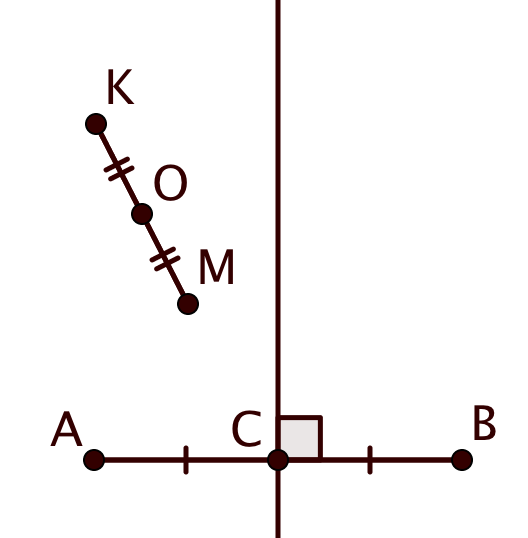
Тогда, так как обе точки и лежат по одну сторону относительно серединного перпендикуляра, то и середина отрезка , точка , также лежит по одну сторону с точкой относительно серединного перпендикуляра к . Значит, по тому же пункту (а), расстояние от до меньше, чем до , или