ГМТ, расположение объектов на плоскости
Ошибка.
Попробуйте повторить позже
Дан прямоугольник Найдите ГМТ
, для которых
Подсказка 1
Рассмотрите несколько точек Х, для которых выполняется требуемое условие. Например, точку пересечения диагоналей или какие-то точки на сторонах. Попробуйте предположить, как будет выглядеть ГМТ.
Подсказка 2
Понятно, что середины BC и AD подходят, а также точка пересечения диагоналей. Три этих точки лежат на одной прямой, может тогда проверить выполнение требуемого условия для всех остальных точек этой прямой?
Подсказка 3
Теперь осталось показать, что никакая другая точка не будет подходить. Рассмотрите произвольную точку Х, не лежащую на упомянутой прямой, что можно сказать о BX и XC, а о AX и DX, может ли тогда выполняться равенство из условия?
Проведем серединный перпендикуляр к отрезку Так как
— прямоугольник, он также будет являться серединным
перпендикуляром к отрезку
Обозначим этот серединный перпендикуляр через
и покажем, что он и является искомым
ГМТ.
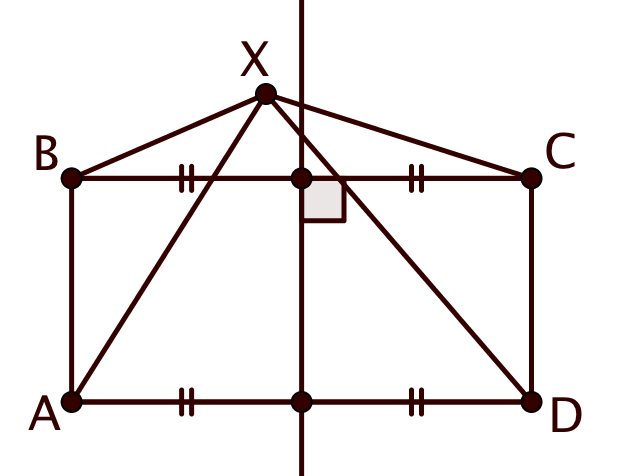
Во-первых, очевидно, что любая точка с подходит: в самом деле, так как
— серединный перпендикуляр, то для всех точек
верно
поэтому
Во-вторых, покажем, что никакая другая точка не подходит. Рассмотрим произвольную точку не на
скажем,
не умаляя общности, что точка
находит по одну сторону относительно
что и точки
и
Тогда выполнено
Поэтому
и необходимое равенство не выполнено. Аналогично для
лежащей по одну
сторону с
и
относительно
выполнено
Таким образом, никакие точки, отличные от
точек
не подходят, значит, искомое ГМТ — прямая
являющаяся серединным перпендикуляром к отрезкам
и
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




