Индукция в графах и теорема Турана
Ошибка.
Попробуйте повторить позже
Дана диаграмма Юнга. Из нее по очереди удаляются клетчатые доминошки так, чтобы в каждый момент времени диаграмма по-прежнему оставалась корректной. Такие удаления проделываются, пока возможно. Оставшуюся диаграмму назовем ядром исходной. Докажите, что определение корректно, то есть результат процесса не зависит от выбора доминошек.
Подсказка 1
Ясно, что любой процесс удаления доминошек конечен. Рассмотрим граф, в котором вершины помечены диаграммами юнга, а ребра соответствуют возможности перехода от одной диаграмме к другой за 1 шаг. Всегда ли у двух прямых потомков одной вершины есть общий потомок?
Подсказка 2
Если доминошки, затрагиваемые при удалениях в переходах к этим потомкам, не пересекаются, то это, очевидно, верно. А что делать с пересекающимися доминошками?
Подсказка 3
Для удаляемой доминошки верно, что справа и сверху от нее клеток нет, и доминошки могут пересекаться только по одной клетке, то есть они образуют уголок. Тогда можно удалить доминошку, стоящую рядом! Тогда у прямых потомков есть общий предок. Что из этого следует?
Для произвольной диаграммы Юнга рассмотрим доминошки, которые можно удалить, не потеряв корректности диаграммы. Для такой
пары клеток верно, что сверху и справа от нее нет клеток. Заметим, что если две такие доминошки не пересекаются, то мы можем их
удалить последовательно и получить одну и ту же диаграмму. А пересекаются они только в угле, как на картинке. Тогда удалим удалим
квадрат двумя способами: при помощи удаления двух вертикальных доминошек и при помощи двух горизонтальных доминошек, и
получим одну и ту же диаграмму Юнга.
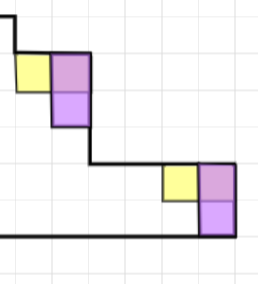
Рассмотрим граф состояний диаграмм Юнга с переходами в виде удаления доминошек, так как клеток конечное число, то все пути конечны, а по доказанному выше он удовлетворяет Diamond-лемме, значит, конечное состояние — единственно.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




