Индукция в графах и теорема Турана
Ошибка.
Попробуйте повторить позже
Дан конечный граф в вершинах которого расставлены вещественные веса (в вершине с номером
вес
Каждую минуту выбирается
произвольная вершина
с отрицательным весом
Ее вес заменяется на
а к весам всех ее соседей прибаляется
Процесс
заканчивается, когда веса всех вершин неотрицательны. Известно, что из исходной конфигурации процесс заканчивается в любом
случае.
(a) Докажите, что результат не зависит от порядка действий;
(b) Докажите, что количество шагов также не зависит от порядка действий.
Подсказка 1
Пусть состояние графа — пара из графа и количества операций, произведенных на нем. Пути в графе, очевидно, конечны. Попробуем доказать, что применима Diamond-лемма. Что тогда нужно доказать?
Подсказка 2
Верно! Нужно показать, что для пары состояний, полученных операциями над вершинами a, b из состояния t найдется общее состояние t'. Если a и b несмежны, то это очевидно. А что нужно сделать, если они все-таки смежны?
Подсказка 3
Пусть C — все вершины, смежные и с a, и c b, A — смежные только с a и B — смежные только с b. Вес в вершине a обозначим r, а в вершине b — m. С помощью операций из условия задачи легко получить вес в a, равный -m, в b - вес -r, вес 2(r+m) в вершинах C и r+m во всех вершинах A и B, проводя операцию сначала над b, а затем над a. А можно ли добиться того же результата, начиная в другом состоянии?
Рассмотрим граф состояний исходного графа. Под состоянием будем иметь в виду пару из получившегося графа и количества операций
на нем произведенных. Так как процесс в любом случае заканчивается, то в этом графе пути конечны.
Для применения Diamond-леммы необходимо показать, что для пары состояний полученных операциями над вершинами
из
состояния
найдется общее состояние
— и
не смежны, тогда преобразования над
и
коммутируют, так как не влияют друг на друга. Результат одинаков при
любом порядке.
— и
смежны, тогда при из
при помощи последовательности операций на рисунках (сначала провели операцию над вершиной
затем над
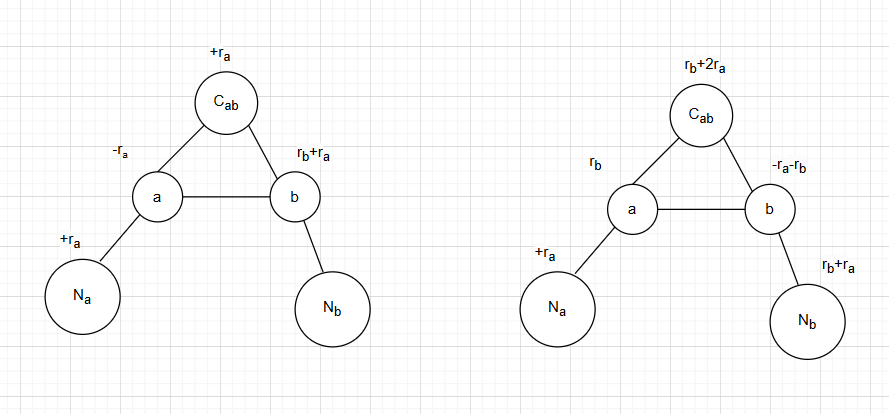
Обозначим — вершины смежные и с
и с
— смежные только с
— только с
Вес в вершине
—
в
—
Тогда после описанных выше операций получим веса:
- в
- в
- в
вес изменится на
- в
вес изменится на
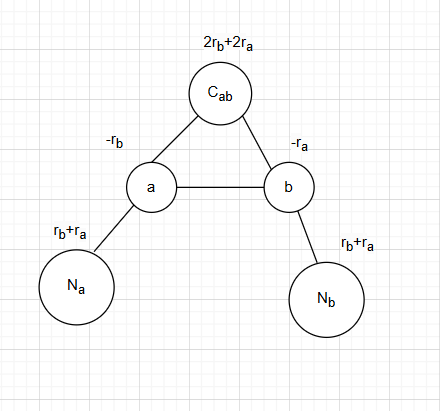
Аналогично при помощи последовательных операций над придем к такому же состоянию из
Причем количество операций в
обоих случаях одинаково, тогда данное состояние
потомок
в графе состояний, значит, верна Diamond-лемма. Тогда есть
единственное конечное состояние
с
произведёнными операциями, не зависящее от порядка операций и любой путь до него будет
длины
Получается оба пункта доказаны.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




