Двойные отношения и гармонические четвёрки
Ошибка.
Попробуйте повторить позже
Дан угол с вершиной и внутри него точка
Рассмотрим такие точки
на разных сторонах данного угла, что углы
и
равны. Докажите, что все прямые
проходят через одну точку (или параллельны).
Подсказка 1.
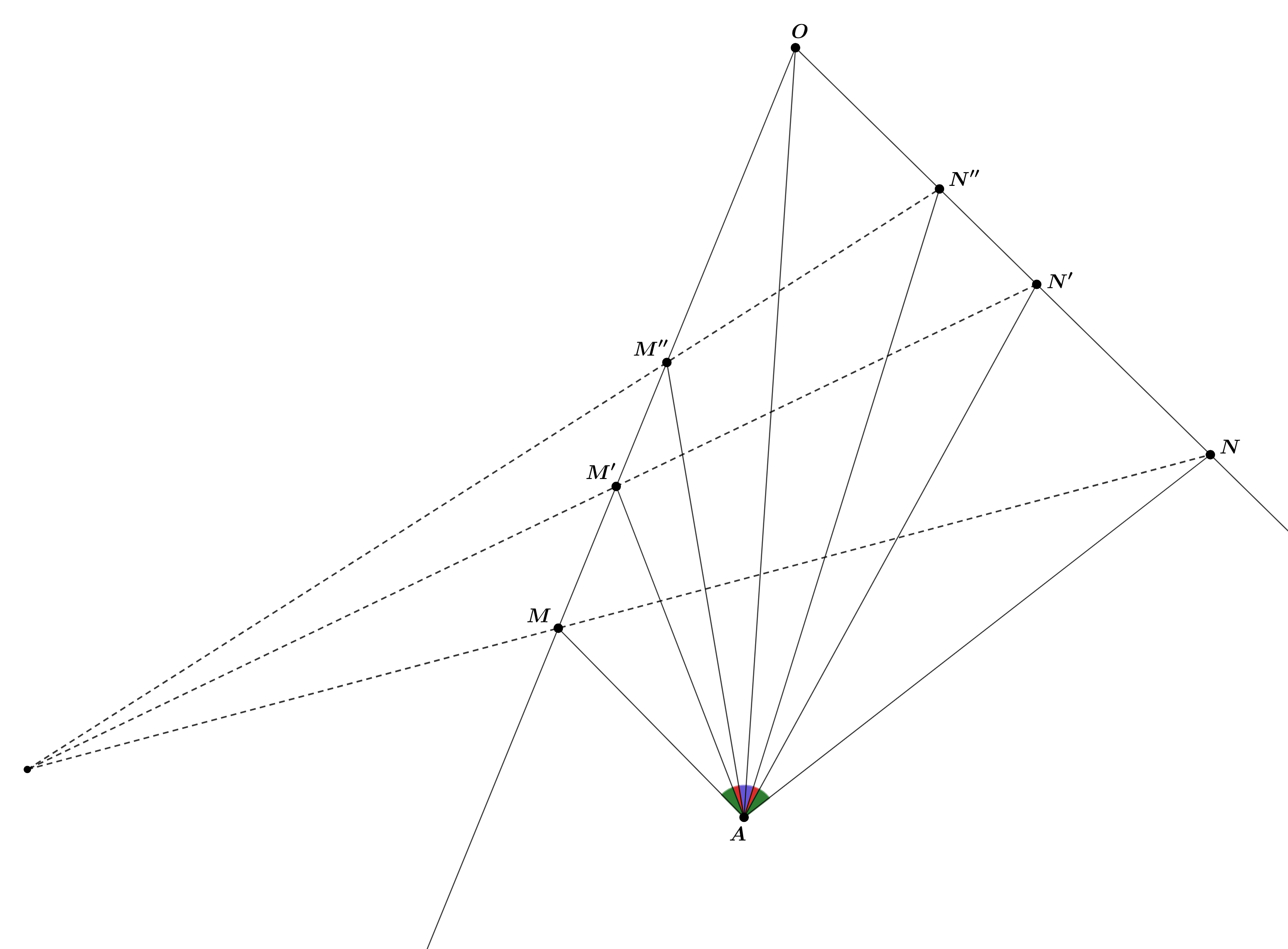
Для доказательства утверждения задачи достаточно понять, что если взять три положения точек (M,N), (M',N'), (M'', N"), то прямые MN, M'N', M''N'' пересекутся в одной точке. Это доказать легче, ведь не приходится работать со всеми положениями точек M и N, а всего с тремя. Как это можно доказать?
Отметим еще точки и
удовлетворяющие тому же условию. Достаточно доказать, что прямые
пересекаются в одной точке. Для этого достаточно проверить, что
что
равносильно равенству
которое верно в силу того, что двойное отношение
прямых определяется через синусы углов между ними, а у этих четверок прямых все соответственные углы между ними
равны.
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




