Двойные отношения и гармонические четвёрки
Ошибка.
Попробуйте повторить позже
Продолжения противоположных сторон выпуклого четырехугольника пересекаются в точках
и
Через точку
пересечения его диагоналей проводится прямая, параллельная
Докажите, что отрезок этой прямой, заключенный внутри
четырехугольника, делится точкой
пополам.
Подсказка 1
Двойные отношения нередко используют для того, чтобы показать, что некоторая точка является серединой отрезка. Как их рассмотрение помогает в данной ситуации?
Подсказка 2
Достаточно показать, что двойное отношение точек (F, E; O, S), где S — бесконечная точка лежащая на прямой направления FE, равно -1. Как это можно сделать?
Подсказка 3
Спроецировать какую-нибудь гармоническую четверку соответственно в данные точки. Для какой четверки это можно сделать?
Подсказка 4
Спроецировать какую-нибудь гармоническую четверку соответственно в данные точки. Для какой четверки это можно сделать?
Подсказка 5
Ясно, что центр проецирования и одна из точек четверки должны лежать на прямой, параллельной прямой FE. Такая прямая на рисунке уже есть - это прямая PQ.
Подсказка 6
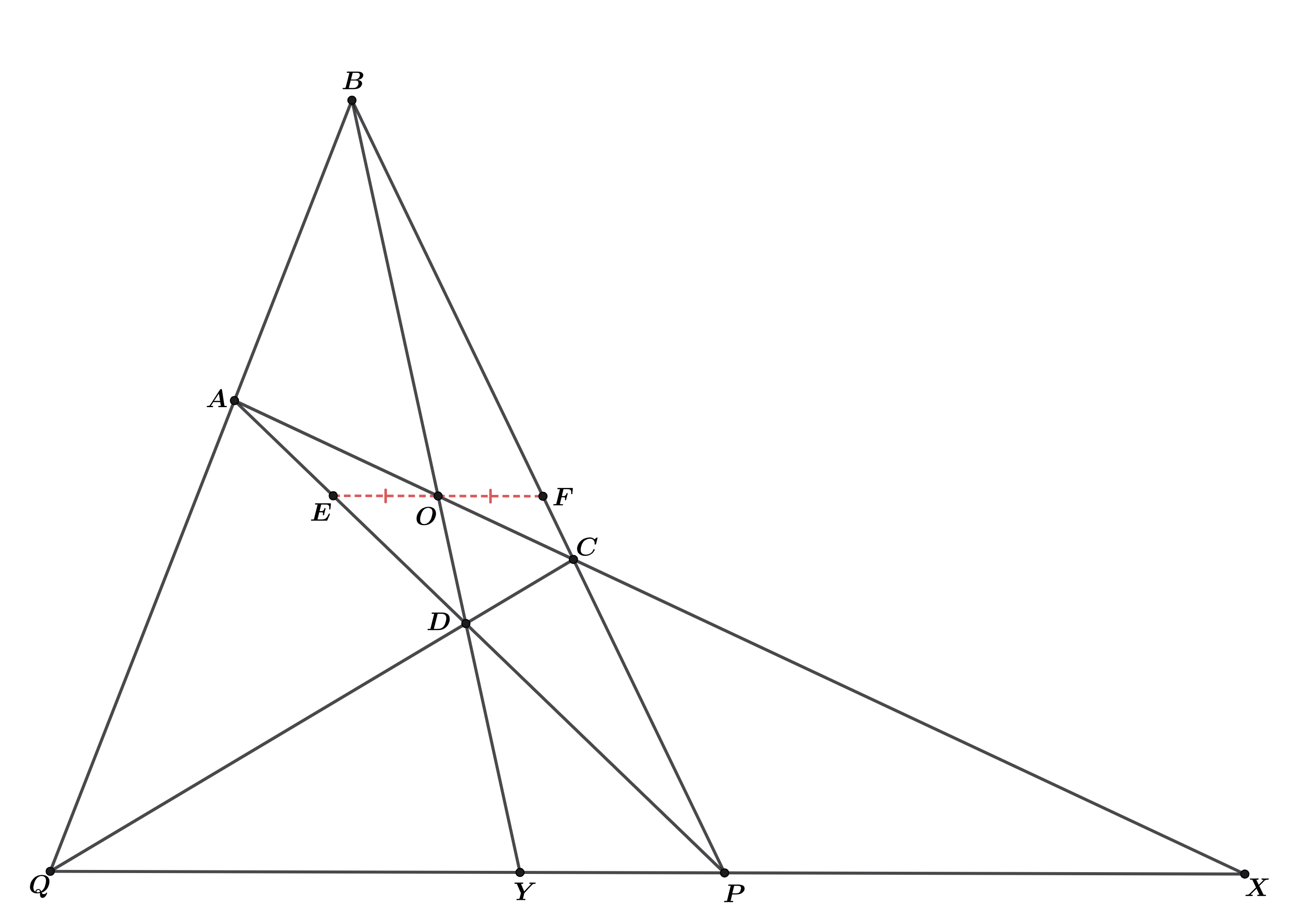
По теореме о полном четырехстороннике точки A, O, C, X, где X — точка пересечения прямой PQ и AC, образуют гармоническую четверку. Осталось заметить, что при проецировании с центром в точке P прямой AC на прямую FE четверка (C, A, O, X) переходит в четверку (F, E, O, S), то есть двойное отношение второй равно -1.
Обозначим через точку пересечения прямых
и
через
— точку пересечения прямых
и
Тогда по теореме о
полном четырёхстороннике четвёрка точек
гармоническая. Спроецируем эту четверку на прямую
через точку
Получим, что четвёрка точек
гармоническая. Обозначим точки пересечения прямой, проходящей через
параллельно
и четырёхугольника
через
и
После проецирования четвёрки
на
через точку
получаем,
что четверка прямых
— гармоническая. Но
тогда
— середина
что и требовалось
доказать
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




