Бесконечные конструкции (игры, клетки, множества)
Ошибка.
Попробуйте повторить позже
Можно ли так раскрасить все клетки бесконечной клетчатой плоскости в белый и черный цвета, чтобы каждая вертикальная прямая и каждая горизонтальная прямая пересекали конечное число белых клеток, а каждая наклонная прямая — конечное число черных?
Источники:
Введем такую систему координат чтобы вертикальные и горизонтальные линии сетки имели уравнения
(
— целое) и
(
— целое). Раскрасим в черный цвет те и только те клетки, все точки которых удовлетворяют одному из четырех неравенств
или
(см.рис.), остальные клетки покрасим в белый цвет.
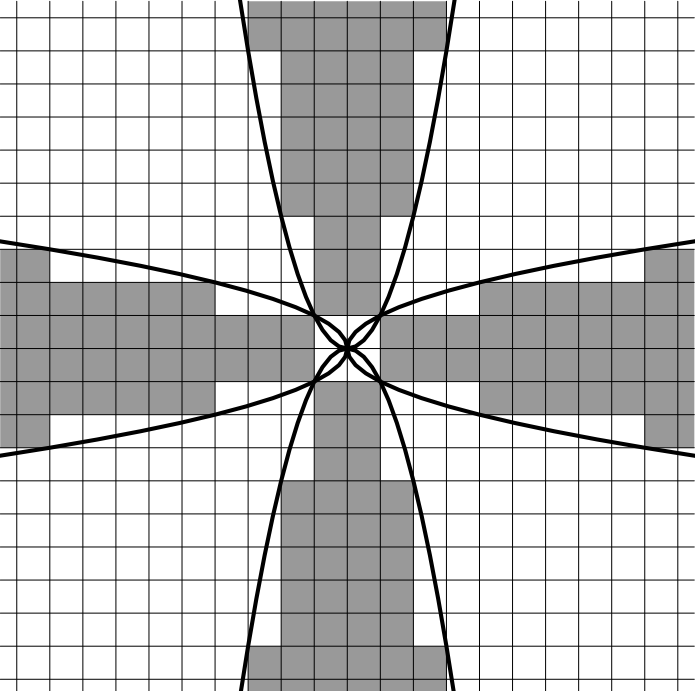
Тогда всякая вертикальная прямая будет пересекать конечное число белых клеток между параболами всякая горизонтальная
прямая будет пересекать конечное число белых клеток между параболами
Заметим также, что всякая наклонная прямая будет
пересекать лишь конечное число черных клеток, так как ее пересечение с каждой из областей
может быть либо пустым, либо являться точкой, либо отрезком.
Можно
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




