Бесконечные конструкции (игры, клетки, множества)

Зададим систему координат с точкой начала отсчета в одном из центров клетки доски и осями, параллельными прямым, содержащим стороны клеток. Назовем клеткой клетку, центр которой в заданной системе координат имеет координаты

Зафиксируем натуральное число Приведем стратегию игры за первого игрока. Проведем итерации следующего алгоритма:

Найдем натуральное число такое, что в каждом из множеств клеток и нет отмеченных.

В каждом из данных множеств отметим клеток крестиком: на каждом четном ходу будет ставить крестик в одну из клеток первого множества, на каждом нечетном — из второго. Так, мы можем отметить по крайней мере крестиков в каждом множестве, что при достаточно большом больше, чем

Рассмотрим клетчатую бумагу после последней итерации алгоритма. Назовем множество клеток для всех особенным квадратом.

В каждую клетку особого квадрата запишем число равное количеству пар клеток, которые стоят в одной диаогнале, а на пересечении соответствующей вертикале и горизонтале стоит (см. рис).

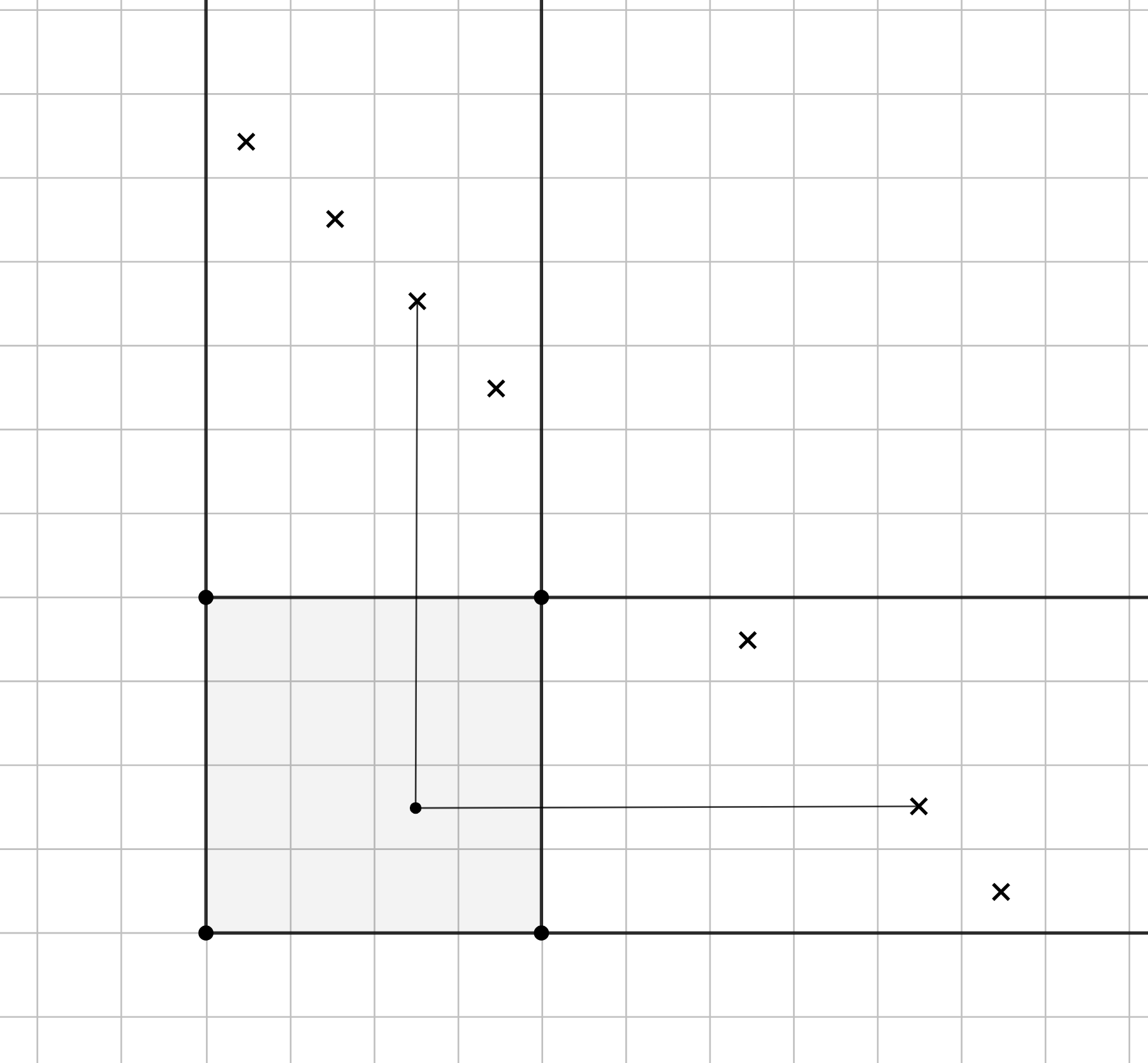
Во-первых, для любой клетки число в не превосходит числа — количества диагоналей, на которой расставлены крестики. Во-вторых, сумма всех чисел в особенном квадрате не меньше, чем — число всевозможных пар клеток, стоящих на одной диагонали.

После последней итерации алгоритма в особенном квадрате не более

клеток, отмечено ноликом — это общее количество ходов, которое было соверешенно на данный момент. Достаточно показать, что существует не меньше клеток особенного квадрата, число которых не меньше 101, тогда по принципу Дирихле, найдется клетка, число в которой хотя бы 101, наконец, поставив крестик в нее, мы добьемся победы на следующем ходу.

Предположим противное. Тогда существует не более клеток, числа каждой из которых не превосходят следовательно, в остальных клетках сумма не превосходит Таким образом, сумма чисел всех клеток в особенном квадрате не превосходит

но, как мы выяснили раннее, это число не меньше, чем что при достаточно больших это невозможно.