.07 Электродинамика. Магнетизм
Ошибка.
Попробуйте повторить позже
Три параллельных длинных прямых проводника 1, 2 и 3 перпендикулярны плоскости рисунка и пересекают её в вершинах
равностороннего треугольника со стороной . Токи в проводниках сонаправлены и равны
. Опираясь на законы
электродинамики, определите направление вектора индукции результирующего магнитного поля в точке О – центре треугольника.
Как изменится направление вектора индукции результирующего магнитного поля в точке О, если направление электрического тока
в проводнике 3 изменить на противоположное?

Источники:
Вокруг каждого из проводников возникает магнитное поле, линии индукции которого являются окружностями. Направление линий
индукции магнитного поля определяется правилом буравчика (см. рис. а). Вектор индукции результирующего магнитного поля в
точке О, определяется принципом суперпозиции: , где
,
и
– векторы индукции магнитных полей в
точке О, созданных каждым проводником отдельно. Поскольку точка О равноудалена от каждого проводника и по проводникам
протекают токи одинаковой силы, то
.
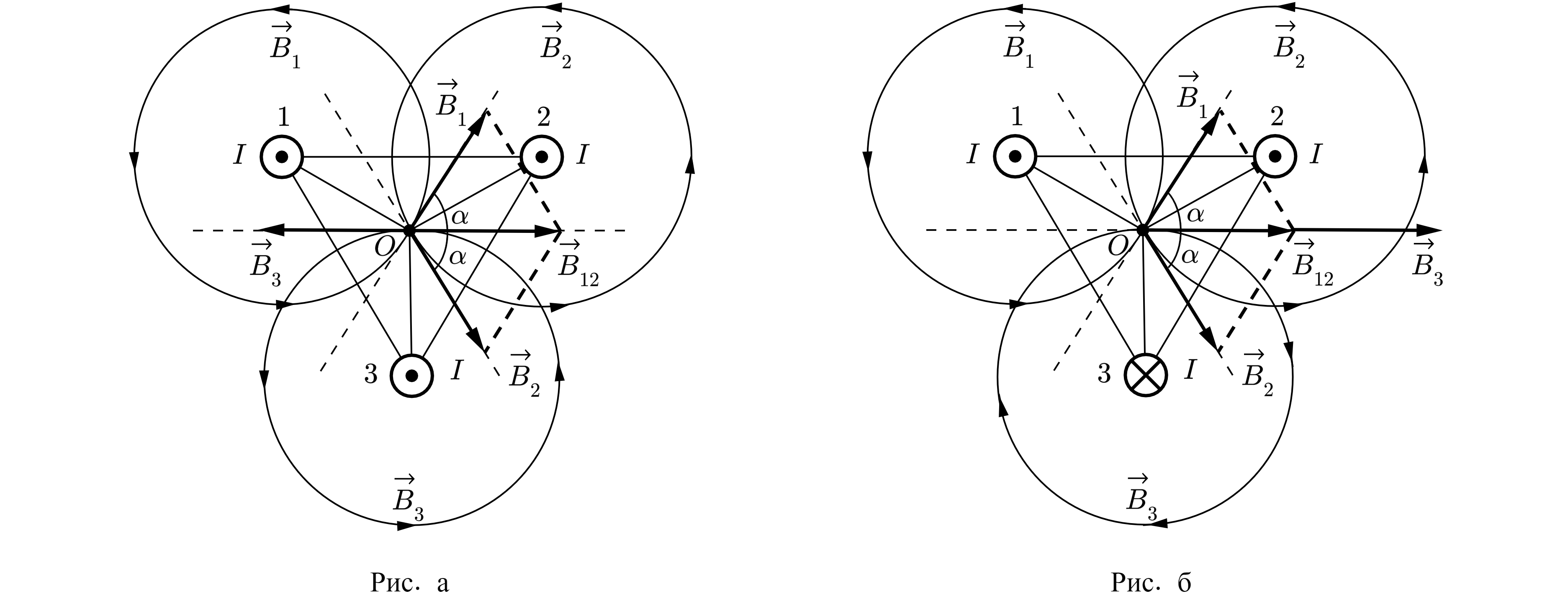
Из геометрических построений видно, что угол между векторами и
составляет 120
, а, значит,
.
Следовательно,
Таким образом, Если направление электрического тока в проводнике 3 изменить на противоположное,
то вектор магнитного поля, созданного этим проводником в точке О, будет направлен горизонтально вправо (см. рис.
б).
Таким образом,
| Критерии оценивания выполнения задачи | Баллы |
| Приведено полное правильное решение, включающее правильный | 3 |
| ответ (в данном случае: сказано как меняется направление вектора магнитной индукции) | |
| и исчерпывающие верные рассуждения с прямым указанием | |
| наблюдаемых явлений и законов (в данном случае: с использованием правила буравчика (или иным верным способом) определено направление индукции магнитного поля, создаваемого каждым проводником в точке О, сделан правильный вывод о том, что при равенстве токов в проводниках и расстояний от них до точки О, индукции магнитных полей проводников с токами равны по абсолютной величине, с использованием принципа суперпозиции магнитных полей найдено направление вектора индукции результирующего магнитного поля в точке О как при первоначальном направлении токов в проводниках, так и при изменении направления тока в третьем проводнике) | |
| Дан правильный ответ, и приведено объяснение, но в решении | 2 |
| имеется один или несколько из следующих недостатков. | |
|
| |
| В объяснении не указано или не используется одно из физических | |
| явлений, свойств, определений или один из законов (формул), | |
| необходимых для полного верного объяснения. (Утверждение, | |
| лежащее в основе объяснения, не подкреплено соответствующим | |
| законом, свойством, явлением, определением и т.п.) | |
|
И (ИЛИ)
| |
| Указаны все необходимые для объяснения явления и законы, | |
| закономерности, но в них содержится один логический недочёт. | |
|
И (ИЛИ)
| |
| В решении имеются лишние записи, не входящие в решение | |
| (возможно, неверные), которые не отделены от решения | |
| и не зачёркнуты. | |
|
И (ИЛИ)
| |
| В решении имеется неточность в указании на одно из физических | |
| явлений, свойств, определений, законов (формул), необходимых для | |
| полного верного объяснения | |
| Представлено решение, соответствующее одному из следующих | 1 |
| случаев. | |
| Дан правильный ответ на вопрос задания, и приведено объяснение, | |
| но в нём не указаны два явления или физических закона, | |
| необходимых для полного верного объяснения. | |
|
ИЛИ
| |
| Указаны все необходимые для объяснения явления и законы, | |
| закономерности, но имеющиеся рассуждения, направленные | |
| на получение ответа на вопрос задания, не доведены до конца. | |
|
ИЛИ
| |
| Указаны все необходимые для объяснения явления и законы, | |
| закономерности, но имеющиеся рассуждения, приводящие | |
| к ответу, содержат ошибки. | |
| Указаны не все необходимые для объяснения явления и законы, | |
| закономерности, но имеются верные рассуждения, направленные на | |
| решение задачи | |
| Все случаи решения, которые не соответствуют вышеуказанным | 0 |
| критериям выставления оценок в 1, 2, 3 балла | |
| Максимальный балл | 3 |
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




