Алгебраические текстовые задачи на Иннополисе
Ошибка.
Попробуйте повторить позже
Во время собеседования при приеме на работу в разных IT-компаниях любят задавать разные тестовые нестандартные задачи для проверки творческих способностей кандидата на работу. Одна из таких популярных тестовых задач следующая (см. рисунок):
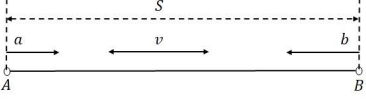
Точки и
двигаются на встречу друг-другу (обычно говорят о двух «путниках») со скоростями
и
соответственно, а между
ними все время «летает» со скоростью
и
еще одна точка (обычно говорят о «мухе», которая летает с носа одного путника
на нос другого путника без задержек на носу ни одного из путников). Начальное расстояние между точками
и
равно
Вопрос: какое расстояние пролетит точка-муха от момента начала движения точек-путников до момента их
встречи?
Так вот, в этой задаче вам сначала надо ответить на вопрос, сформулированный в тестовой задаче: какое расстояние пролетит точка-муха от момента начала движения точек-путников до момента их встречи? Далее, вам надо ответить на следующий вопрос (и доказать ответ!): конечное или бесконечное число полетов между точкам-путниками совершит точка-муха от момента начала движения до момента встречи точек-путников?
И, наконец, вам надо ответить на еще один вопрос. Пусть в начальный момент точка-муха находилась в точке Какое суммарное
расстояние пролетит точка-муха, когда движется от
до
А какое суммарное расстояние пролетит точка-муха, когда движется от
до
Источники:
Вопрос 1, подсказка 1
Сначала можно вычислить время, которое будет летать точка-муха, а потом уже найти расстояние.
Вопрос 2, подсказка 1
Предположим, что точка-муха совершила конечное число полетов, тогда мы либо докажем это, либо получим противоречие.
Вопрос 2, подсказка 2
Попробуйте рассмотреть последний полет точки-мухи.
Вопрос 2, подсказка 3
Пусть последний полет был от точки А. Какие будут скорости у точки А и у точки-мухи?
Вопрос 2, подсказка 4
У точки-мухи будет скорость v, у точки А — a. Какая из этих точек прилетит раньше в точку встречи точек-путников?
Вопрос 2, подсказка 5
Сравните скорости a и v, опираясь на условие, и проведите аналогичные рассуждения в случае, если последний полет точки-мухи происходит от точки B.
Вопрос 3, подсказка 1
Давайте попробуем составить формулы расстояний перелетов в общем виде. Для этого можно посчитать расстояния в конкретных ситуациях.
Вопрос 3, подсказка 2
В некоторый момент времени точка-муха находится в точке А, пусть в этот момент расстояние между A и B равно p₀. Через какое время точка-муха окажется в точке B?
Вопрос 3, подсказка 3
t₁ = p₀ / (v + b). Какое расстояние при этом пролетит точка-муха?
Вопрос 3, подсказка 4
w₁ = t₁v = p₀v / (v + b). Чему будет равно расстояние между точками A и B после полета?
Вопрос 3, подсказка 5
p₁ = p₀ - t₁(a + b) = p₀ ⋅ (v - a) / (v + b). Через какое время точка-муха вновь окажется в точке А?
Вопрос 3, подсказка 6
t₂ = p₁ / (v + a) = p₀ ⋅ (v - a) / ((v + a)⋅(v + b)). Какое расстояние она пролетит от B к A?
Вопрос 3, подсказка 7
w₂ = t₂v = p₀ ⋅ (v - a) ⋅ v / ((v + a)⋅(v + b)). Какое расстояние между точками A и B после этого?
Вопрос 3, подсказка 8
p₂ = p₁ - t₂(a + b) = p₀ ⋅ (v - a)(v - b) / ((v + a)(v + b)). Посмотрите на полученные результаты и попробуйте записать в общем виде формулы для расстояний между точками A и B до и после k-го перелета.
Вопрос 3, подсказка 9
Теперь вспомним, что мы хотим найти. Запишите формулы для расстояний, которые будет пролетать точка-муха.
Вопрос 3, подсказка 10
Рассмотрим случай, когда точка-муха летит от A к B. Заметьте, что расстояния, которые будет пролетать точка-муха, образуют бесконечно убывающую геометрическую прогрессию.
Вопрос 3, подсказка 11
Ее суммой и будет суммарное расстоние, которое пролетит точка-муха от A до B. Чтобы найти суммарное расстояние, которое пролетит точка-муха от B к A, для начала посчитайте общее расстояние, которое пролетит точка-муха.
Первый вопрос.
Общее время движения точек-путников
поэтому расстояние, которое пролетит точка-муха за это время
Второй вопрос.
Давайте предположим, что точка-муха совершит некоторое конечное число полетов между точками-путниками. Тогда либо мы докажем это, либо прийдем к противоречию и получим, что полетов было бесконечное количество.
Рассмотрим последний полет точки-мухи между точками-путниками. Если это был полет от точки движущейся направо со
скоростью
то, так как это был последний полет, точка-муха тоже летит направо со скоростью
и прилетает в точку встречи
точек-путников не раньше точки
то есть скорость точки-мухи
которая не больше скорости
Получаем противоречие с тем, что Аналогично получаем противоречие в случае, если последний полет точки-мухи происходит от
точки
Следовательно, предположение о конечном числе полетов неверно.
Третий вопрос.
Пусть в некоторый момент времени точка-муха находится в точке и в это время расстояние между точками
и
равно
Тогда точка-муха окажется в точке
спустя время
при этом точка-муха пролетит расстояние
в направлении от к
а расстояние между точками
и
после полета будет равно
Точка-муха вновь окажется в точке спустя время
Она пролетит в направлении от к
После этого расстояние между точками и
будет равно
Следовательно, для любого мы имеем: расстояние между точками
и
после
перелета
-
от
до
равно
-
от
до
равно
Теперь заметим, что для любого расстояние между точками перед
перелетом
-
от
до
равно
-
от
до
равно
Тогда для любого расстояние, которое пролетит точка-муха в
раз,
-
от
до
равно
-
от
до
равно
— бесконечно убывающая геометрическая прогрессия с первым членом
и знаменателем
Сумма прогрессии равна
Это и есть суммарное расстояние, которое пролетит точка-муха, когда движется от до
Так как общее расстояние, которое пролетит точка-муха, равно
то, следовательно, суммарное расстояние, которое пролетит точка-муха, когда движется от к
равно
1) 2) Бесконечное; 3)
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




