Планиметрия на КФУ

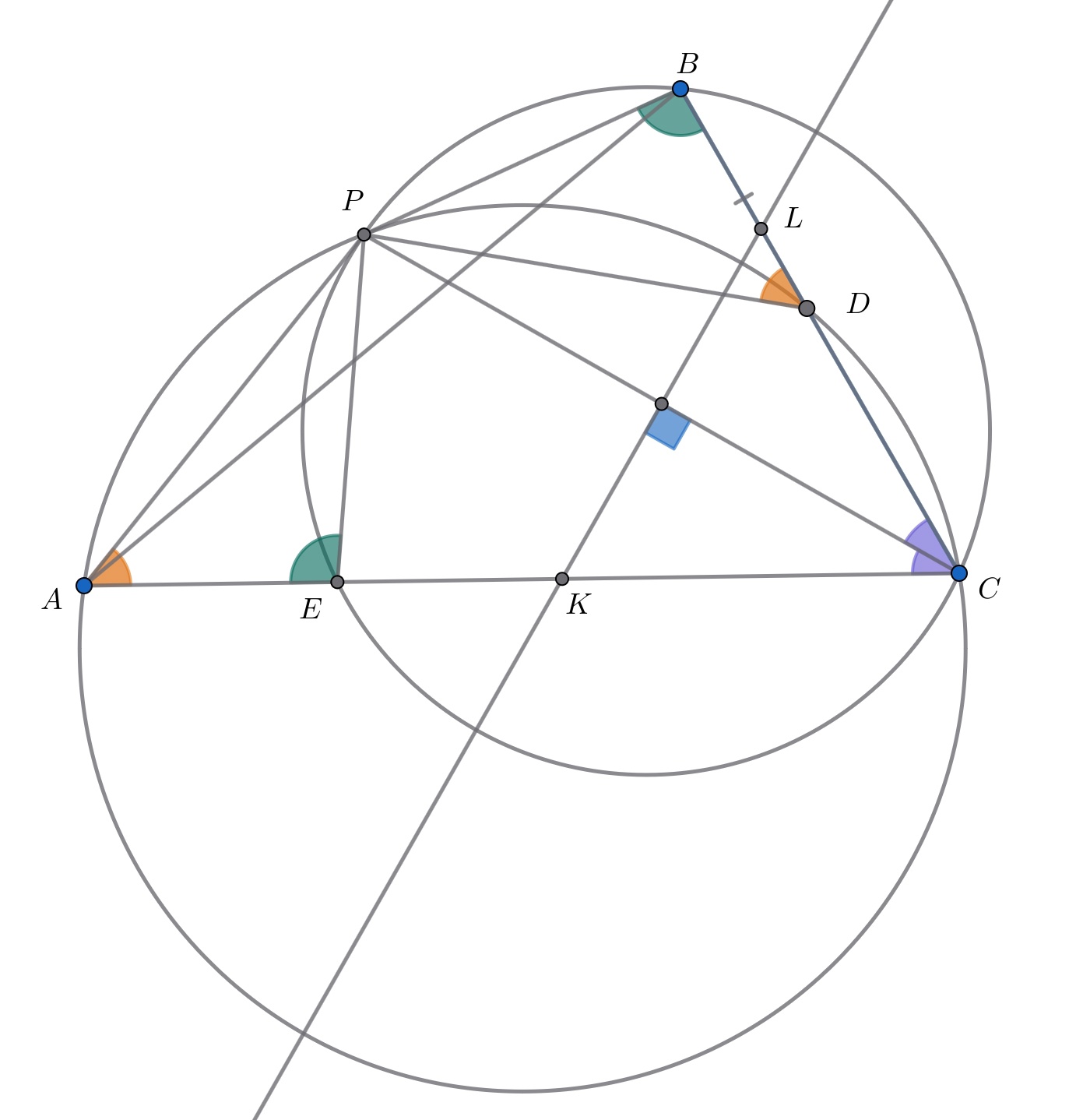
Пусть описанные окружности треугольников и пересекаются в точках и (см. рис.). Докажем, что и, значит, искомое отношение равно

Как известно, линия, соединяющая центры описанных окружностей и перпендикулярна общей хорде этих окружностей, так что отрезки и перпендикулярны.

Так как точки принадлежат одной окружности, сумма углов и равна Но сумма смежных утлов и тоже равна значит, Аналогично, Из этих двух равенств, а также из условия следует, что треугольники и равны. Отсюда Из равенства этих хорд следует равенство соответствующих дуг, а значит, и равенство вписанных углов и

Таким образом, треугольник — равнобедренный, так как является биссектрисой и высотой; поэтому

Замечание.

Тот факт, что — биссектриса, можно доказать и по-другому. По теореме о секущей

и

Отсюда

То есть прямая делит сторону на отрезки, пропорциональные двум другим сторонам треугольника. Значит, — биссектриса, что и требовалось.