Планиметрия на КФУ
Ошибка.
Попробуйте повторить позже
Задан выпуклый четырехугольник, в нем проведены биссектрисы всех четырех углов. Может ли оказаться, что каждую из сторон (в ее внутренней точке) пересекает хотя бы одна из биссектрис?
Источники:
Подсказка 1
Как биссектрисы должны пересекать стороны?
Подсказка 2
Каждую сторону должна пересечь ровно одна биссектриса. Как могут взаимно располагаться биссектрисы?
Подсказка 3
Например, если в четырёхугольнике ABCD биссектриса ∠A пересекает сторону BC, то биссектриса ∠D должна пересекать сторону AB.
Подсказка 4
А что нам вообще могут дать биссектрисы? Какие у них есть свойства?
Подсказка 5
Рассмотрите диагонали четырёхугольника.
Подсказка 6
Посмотрите, как биссектрисы делят диагонали. Для этого надо воспользоваться свойством биссектрисы об отношении сторон и отрезков в треугольнике.
Если каждую сторону во внутренней точке пересекает какая-то биссектриса, то каждую из них пересекает ровно одна.
Пусть для определенности биссектриса угла пересекает сторону
(длиной
). Биссектриса угла
вообще говоря, может
пересекать
или
но в силу условия пересекает сторону
(длиной
Аналогично получаем, что биссектриса угла
пересекает сторону
(длиной
и биссектриса угла
— сторону
(длиной
Пусть биссектриса угла пересекает диагональ
в точке
а биссектриса угла
в точке
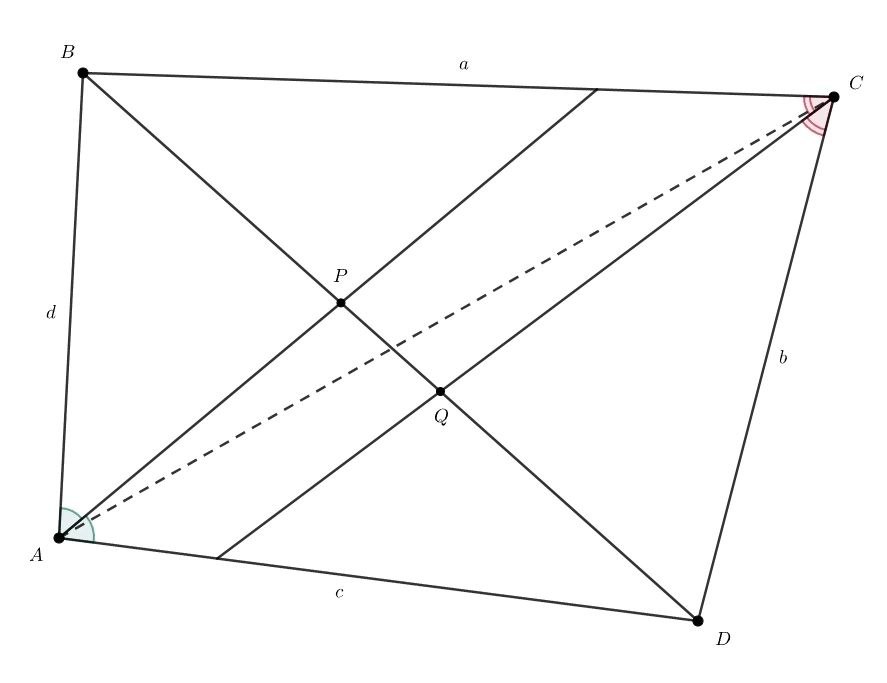
Заметим, что по свойству биссектрисы
Но биссектриса угла пересекает диагональ
ближе к вершине
чем биссектриса угла
Значит,
Аналогичное исследование второй диагонали показывает, что
Пришли к противоречию.
Нет, не может
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




