Планиметрия на КФУ
Ошибка.
Попробуйте повторить позже
В неравнобедренном треугольнике 
провели высоту 
медиану 
и биссектрису 
Точки 
и 
— ортогональные
проекции вершин 
и 
на прямую 
Докажите, что точки 
и 
лежат на одной окружности.
Источники:
Рассмотрим без ограничения общности 
Тогда точка 
лежит внутри треугольника 
, а точка 
вне
его.
Первое решение.
Построим описанную окружность треугольника 
, тогда продолжение биссектрисы 
пересечет ее в точке 
,
являющейся серединой дуги 
. Тогда 
, то есть медиана 
равнобедренного треугольника 
будет также и
высотой.
Так как 
, то получим, что 
. Так как 
аналогично получаем, что
.
Но углы 
равны, как вписанные углы, опирающиеся на одну дугу.
В итоге 
. Но из равенства углов 
следует, что точки 
лежат на одной
окружности.
Второе решение.
Обозначим через 
и 
точки пересечения прямых 
и 
и 
соответственно.
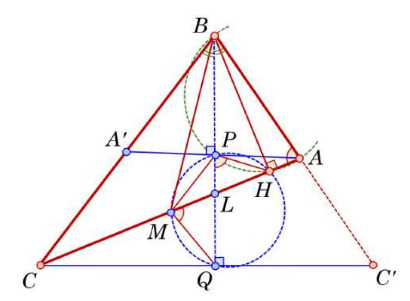
Поскольку 
— биссектриса и 
треугольники 
и 
— равнобедренные, и значит, 
и
В треугольнике 
точки 
и 
— середины сторон 
и 
поэтому 
— средняя линия, и значит, 
Аналогично, 
Следовательно, 
Возможны два случая:
a) 
Точки 
и 
лежат на одной окружности с диаметром 
поэтому четырёхугольник 
— вписанный.
Значит,
Следовательно, точки 
и 
лежат на одной окружности.
б) 
тогда точки 
и 
лежат на одной окружности с диаметром 
поэтому четырёхугольник 
—
вписанный. Значит,
Следовательно, точки 
и 
лежат на одной окружности.
Специальные программы
Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!
Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.
Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.
Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».
Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!
Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!
