Инверсия + симметрия

Пусть Выполним преобразование: инверсию относительно сферы радиуса с центром и затем центральную симметрию с центром — так что переходит в себя, а точки и и и меняются местами. Точка при инверсии переходит в точку сферы диаметрально противоположную точке то есть в противоположную для вершину параллелепипеда, построенного на векторах Пусть это точка тогда Пусть аналогично точка такова, что Имеем (с учётом перпендикулярности векторов

Здесь центр описанной сферы с радиусом Получаем, что и аналогично равны одной и той же величине не зависяшей от тройки хорд.

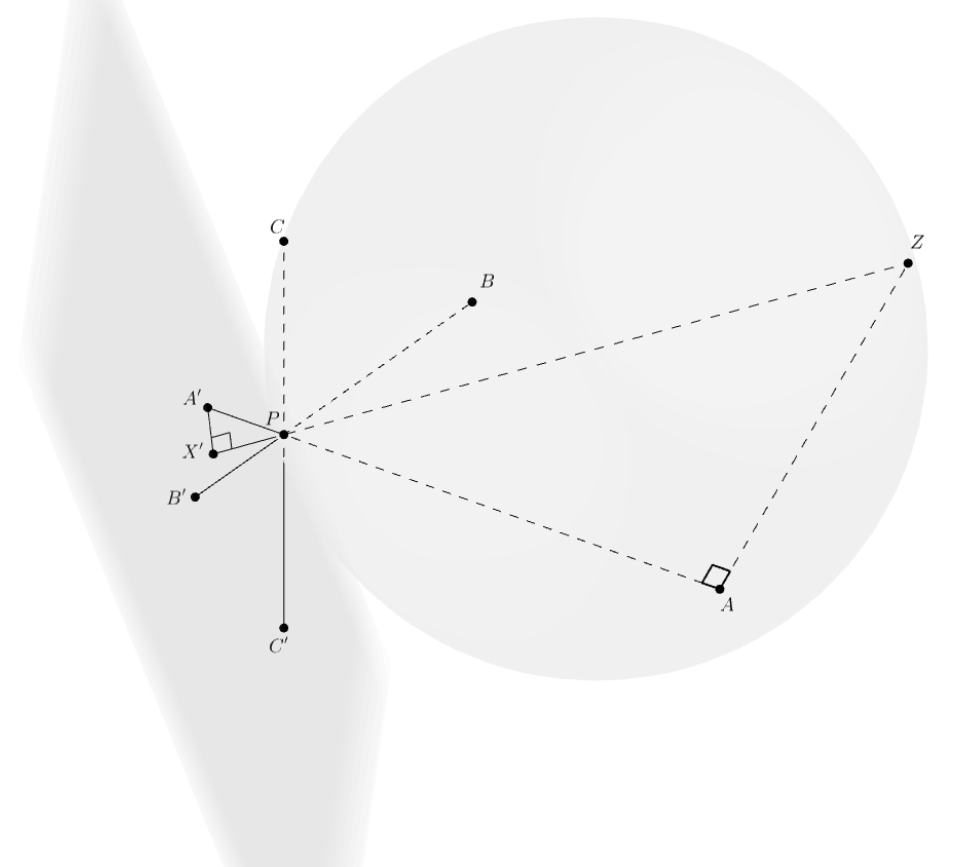
Далее, пусть , — середины хорд, или проекции на соответственно. В силу перпендикулярности хорд:

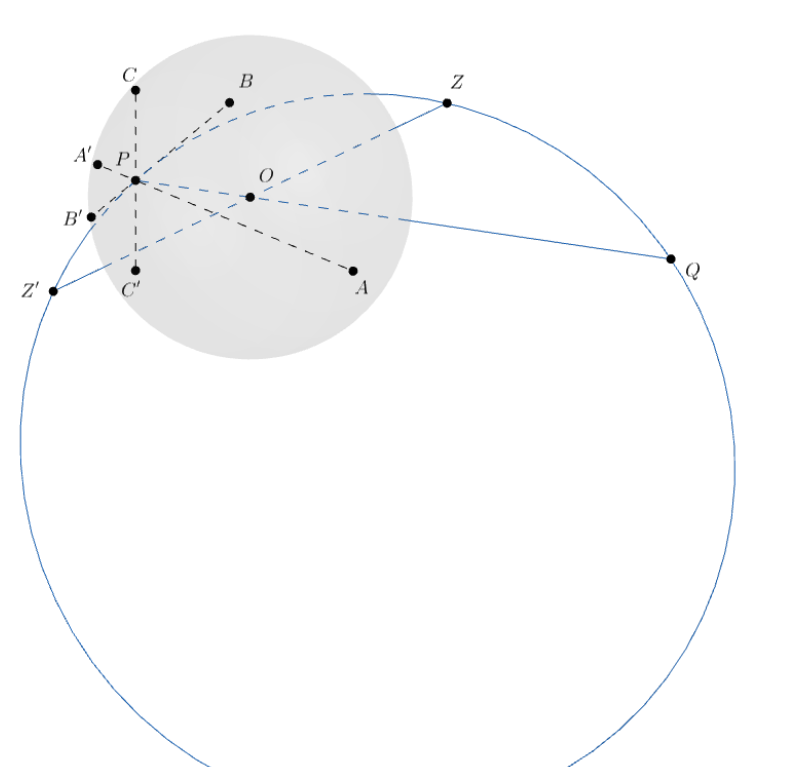
значит, — середина Окружности являющиеся образом прямых при нашем преобразовании, проходят через фиксированную точку, а именно через точку на продолжении отрезка за точку такую, что Значит, и прямые проходят через фиксированную точку.