Инверсия + симметрия

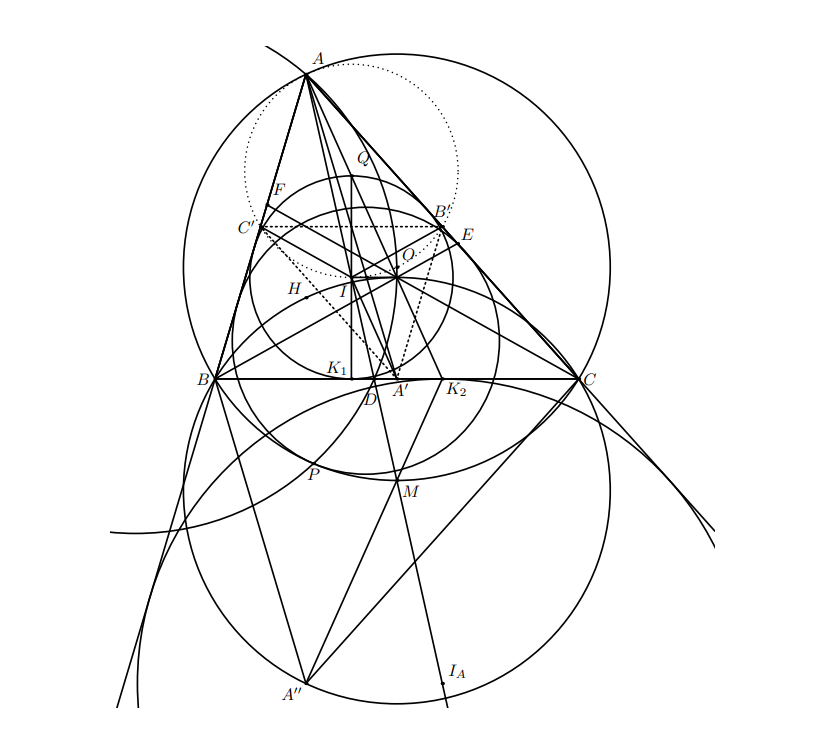
Точка  – точка Нагеля треугольника (точка пересечения трех прямых, соединяющих вершины треугольника с точками касания противоположных сторон с соответствующими вневписанными окружностями; почему все три пересекаются в одной точке – простое упражнение на теорему Чевы). Отметим  – ортоцентр треугольника Так как лежит на окружности Так как точка лежит на описанной окружности треугольника

Пусть  – серединный треугольник,  – центр масс (точка пересечения медиан) треугольника  – инцентр (центр вписанной окружности)

Лемма. Точка является точкой Нагеля для треугольника

Доказательство. Пусть и  – точки касания вписанной и вневписанной окружностей со стороной . Точка  – диаметрально противоположная точке . Поскольку гомотетия с центром в переводит вписанную окружность во вневписанную, точку в точку Значит, точки лежат на одной прямой. Точка является серединой отрезка а точка  – серединой поэтому параллельна Треугольники и гомотетичны с центром в и коэффициентом прямые, соединяющие вершины треугольника с точками касания противоположных сторон с соответствующими вневписанными окружностями, переходят в Значит, точка переходит в точку и является точкой Нагеля для треугольника Дополнительно мы поняли, что делить отрезок в отношении

Гомотетия из доказательства леммы переводит точку в точку Поскольку лежат на одной окружности, то и их образы лежат на одной окружности. и перпендикулярны сторонам и соответственно, поэтому вписанный. Поскольку биссектриса угла дуги и равны, а значит В силу гомотетичности, и является серединой дуги описанной окружности треугольника

Отобразим точки и относительно Назовем образы и Поскольку описанная окружность треугольника симметрична окружности относительно (следствие того факта, что при симметрии попадает на описанную окружность),  – середина дуги окружности Следовательно, лежит на биссектрисе угла

Сделаем симметрию относительно биссектрисы угла и инверсию с таким радиусом, чтобы и где звездочкой обозначаем образ точки под действием композиции преобразований. Точка переходит в точку так как описанная окружность переходит в прямую Точка переходит в точку на прямой которая в два раза ближе к чем образ основания высоты из на Но образ основания высоты это точка на окружности значит образ это Вневписаная окружность, соответствующая вершине переходит в значит переходит в Точки лежат на одной окружности так как прообразы лежат на одной прямой. так как  – центр окружности, содержащей и так как симметрична относительно Так как точка лежит на серединном перпендикуляре к треугольники и равнобедренные и подобные (они имеют общий угол ). Прямые и тем самым, антипараллельны для угла значит лежат на одной окружности. Получается, что пять точек лежат на одной окружности, и, в частности, лежит на описанной окружности