Ортологичные треугольники: теоремы Карно и Штейнера
Ошибка.
Попробуйте повторить позже
В остроугольном треугольнике 
на высоте 
выбрана произвольная точка 
Точки 
и 
— середины сторон 
и 
соответственно. Перпендикуляр, опущенный из 
на 
пересекается с перпендикуляром, опущенным из 
на 
в точке 
Докажите, что точка 
равноудалена от точек 
и 
Заметим, что треугольники 
и 
ортологичны. Действительно, прямые 
проведены из вершин первого
треугольника и перпендикулярны соответственно сторонам 
второго.
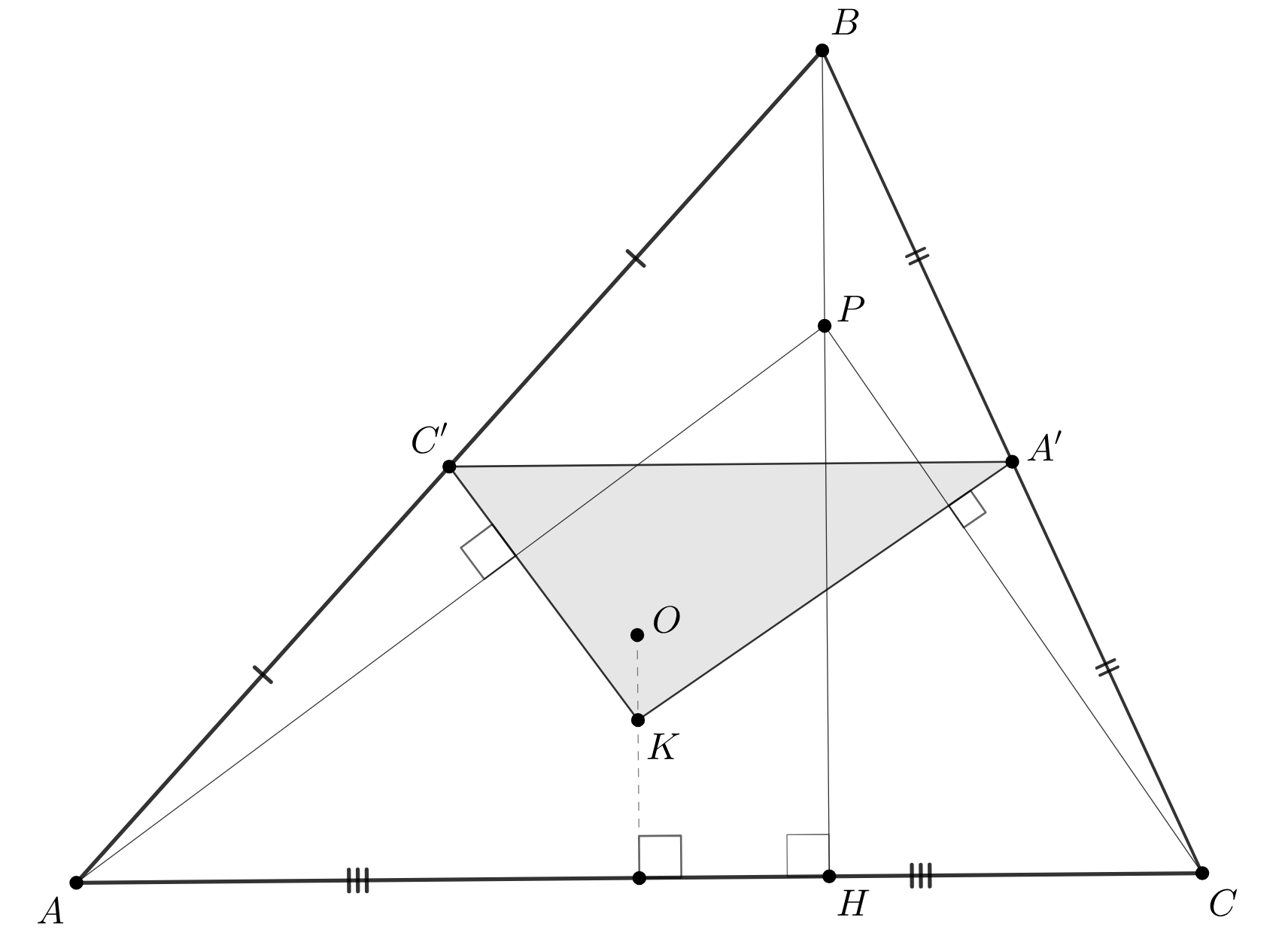
Кроме этого, перпендикуляры в точках 
и 
к сторонам 
и 
являются их серединными перпендикулярами и
пересекаются в точке 
— центре описанной окружности треугольника 
а в силу установленной ортологичности через 
проходит перпендикуляр из точки 
к стороне 
а значит, так же является серединным для нее, что доказывает
требуемое.
Специальные программы
Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!
Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.
Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.
Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».
Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!
Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!
