Сложный вариант осеннего тура Турнира Городов

Первое решение.

Пусть — центры окружностей, — их радиусы. Проведём биссектрису угла (она же — биссектриса угла Пусть она пересекает отрезок в точке

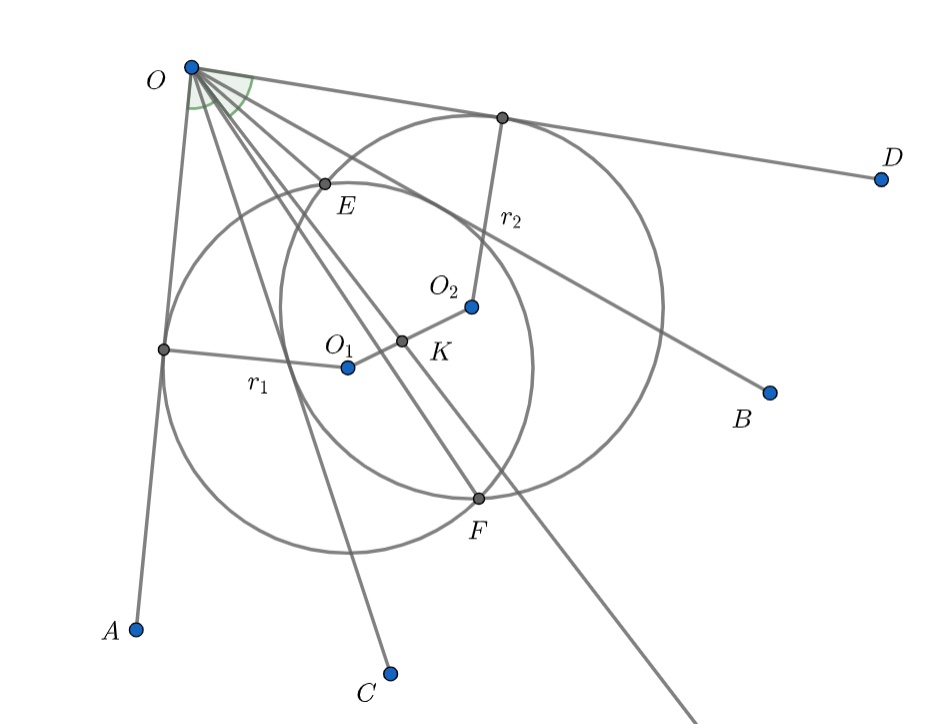
Поскольку

то точки принадлежат одной и той же окружности Аполлония точек и Поскольку — серединный перпендикуляр к то равны хорды этой окружности и Значит, равны и опирающиеся на них вписанные углы и откуда немедленно следует равенство углов и

______________________________________________________________________________________________________________________________________________________

Второе решение.

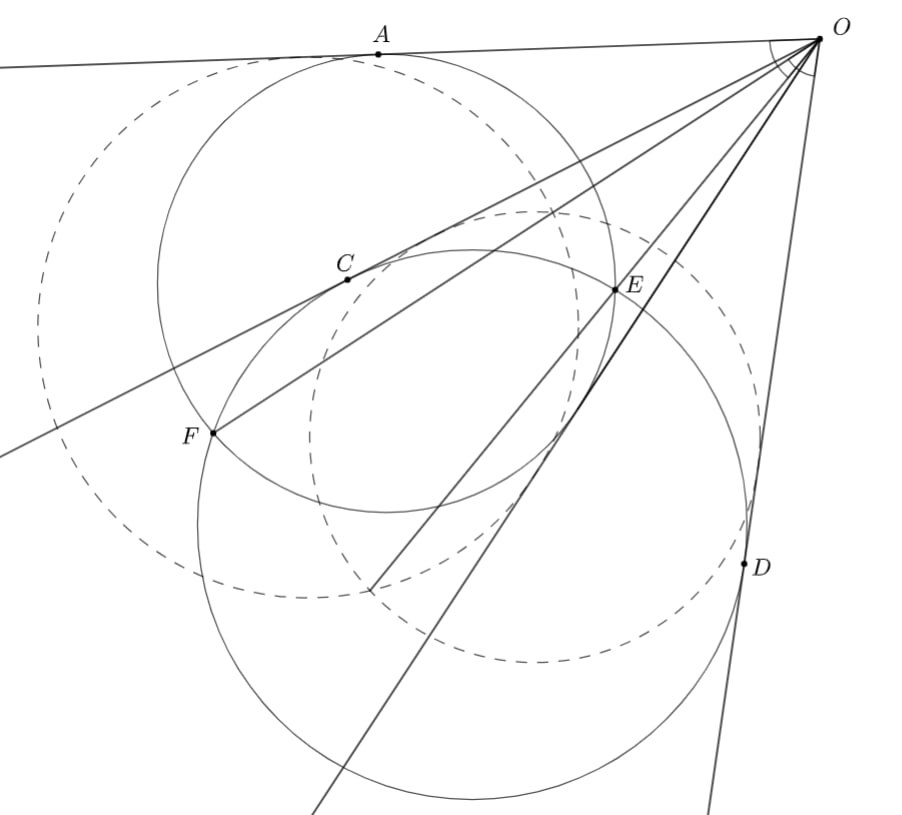
Сделаем инверсию с центром в точке такую, что первая окружность переходит в равную второй. Вторая, соответственно, перейдёт в равную первой. Тогда, с одной стороны, лучи и перейдут в себя, с другой — мы имеем картинку, симметричную исходной относительно биссектрисы угла а значит, она же биссектриса угла откуда