Сложный вариант весеннего тура Турнира Городов
Ошибка.
Попробуйте повторить позже
Боковые стороны 
и 
трапеции 
являются соответственно хордами окружностей 
и 
касающихся друг друга
внешним образом. Градусные меры касающихся дуг 
и 
равны 
и 
Окружности 
и 
также имеют хорды 
и 
соответственно. Их дуги 
и 
расположенные с той же стороны от хорд, что соответствующие дуги первых двух окружностей,
имеют градусные меры 
и 
Докажите, что 
и 
тоже касаются.
Источники:
Пусть 
— точка пересечения прямых 
и 
— точка касания окружностей 
и 
Рассмотрим композицию инверсии с
центром в точке 
радиусом
и симметрии относительно внутренней биссектрисы угла 
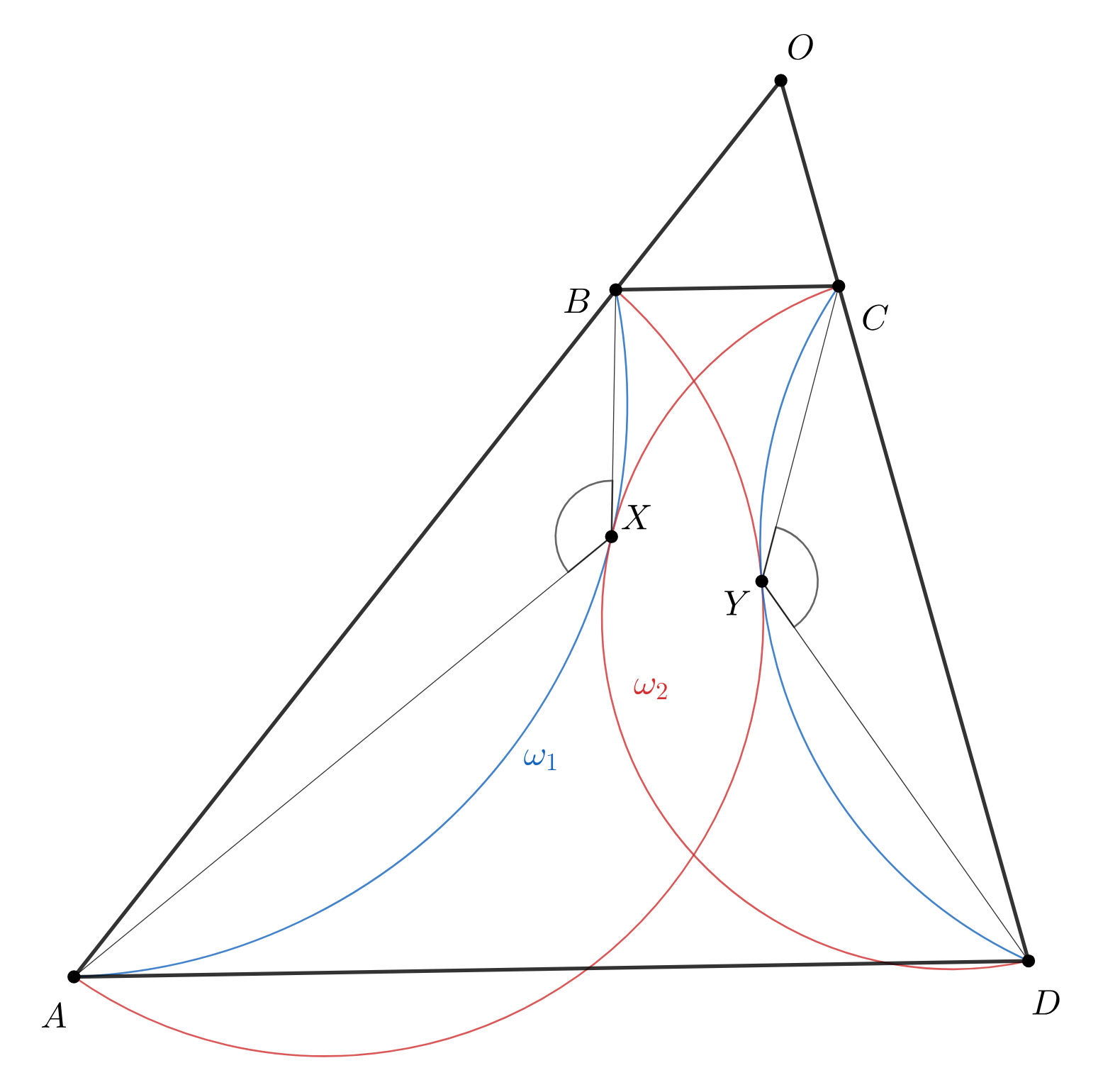
Данное преобразование меняет пары точек 
и 
и 
Пусть 
— образ точки 
тогда окружности 
и 
касаются, т.к. являются образом окружностей 
и 
Осталось заметить, что 
следовательно, 
совпадает с 
аналогично, 
совпадает с
Специальные программы
Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!
Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.
Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.
Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».
Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!
Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!
