№14 из ЕГЭ 2022
Готовиться с нами - ЛЕГКО!
Ошибка.
Попробуйте повторить позже
В кубе точки
и
— середины рёбер
и
соответственно.
a) Докажите, что прямые и
перпендикулярны.
б) Плоскость проходит через точки
и
параллельно прямой
Найдите расстояние от точки
до плоскости
если
а) Пусть отрезки и
пересекаются в точке
Прямоугольные треугольники
и
равны по двум катетам,
значит,
Отрезок — проекция отрезка
на плоскость
Следовательно, по теореме о трёх перпендикулярах прямые
и
перпендикулярны.
![]()
б) Пусть плоскость пересекает ребро
в точке
Прямые
и
лежащие в плоскости
параллельны,
поскольку прямая
лежит в плоскости
параллельной прямой
Следовательно,
а
значит, прямоугольные треугольники
и
подобны по острому углу. Из отношения подобия получаем
Заметим, что поскольку прямая
перпендикулярна прямой
параллельной прямой
Пусть
ребро куба равно
По теореме Пифагора получаем
Кроме того,
Объём пирамиды равен
С другой стороны, объём этой пирамиды равен
Здесь — расстояние от точки
до плоскости
Из равенства
получаем
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Точка — середина бокового ребра
правильной четырёхугольной пирамиды
точка
лежит на
стороне
основания
Плоскость
проходит через точки
и
параллельно боковому ребру
а) Плоскость пересекает ребро
в точке
Докажите, что
б) Пусть Найдите отношение объёмов многогранников, на которые плоскость
разбивает пирамиду
Источники:
а) Пусть — высота пирамиды
Так как пирамида правильная, то
— середина
В плоскости
проведем
Тогда
— средняя линия треугольника
так как
и
значит,
Пусть пересекает
в точке
а
— в точке
Точка
лежит в плоскости
значит, можем
провести прямую
в этой плоскости.
Заметим, что — это плоскость
так как она проходит через точки
и
и содержит прямую
то
есть
Тогда
пересекает
в точке
![]()
Рассмотрим треугольники и
Они равны по второму признаку:
как накрест
лежащие,
как вертикальные. В равных треугольниках соответственные элементы равны, значит,
следовательно,
Рассмотрим треугольники и
Они подобны по двум углам:
и
как
соответственные. Тогда имеем:
Запишем теорему Менелая для треугольника и секущей
б) Пусть
Найдем объем пирамиды
По условию
Значит, по
предыдущему пункту
Тогда площадь треугольника равна
Высота пирамиды равна половине высоты пирамиды
то есть
Тогда объем пирамиды
равен
![]()
Найдем объем пирамиды По предыдущему пункту имеем:
Тогда высота пирамиды равна
Также по предыдущему пункту треугольники
и
подобны с
коэффициентом 2, значит,
Тогда можем найти объем многогранника
Объем всей пирамиды равен
Тогда можем найти объем многогранника
Тогда искомое отношение объемов равно
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
B прямоугольном параллелепипеде на диагонали
отмечена точка
так, что
Точка
— середина отрезка
a) Докажите, что прямая проходит через точку
б) Найдите объём параллелепипеда если длина отрезка
равна расстоянию между прямыми
и
и равна
Источники:
a) Точка — середина диагоналей
и
прямоугольника
. Следовательно, точка
лежит в плоскости
. Треугольники
и
подобны по двум сторонам и углу между ними:
Тогда получаем:
Таким образом, точка лежит на прямой
.
![]()
б) Прямые и
скрещивающиеся, а длина отрезка
равна расстоянию между ними, значит, отрезок
перпендикулярен прямым
и
. Таким образом, прямая
перпендикулярна плоскости
, поскольку она
перпендикулярна лежащим в ней прямым
и
. Следовательно, диагонали прямоугольника
перпендикулярны,
то есть он является квадратом.
Из подобия треугольников и
следует, что
Отрезок — высота прямоугольного треугольника
. Получаем:
Тогда
Таким образом, в прямоугольном параллелепипеде все рёбра равны
. Следовательно, его объём равен
.
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Дана четырехугольная пирамида в основании которой лежит трапеция
Известны ее основания
На ребре
отмечена точка
такая, что
на ребре
отмечена точка
такая, что
плоскость
пересекает ребро
в точке
а) Докажите, что
б) Найдите отношение объемов многогранников, на которые плоскость делит пирамиду.
Источники:
а) Пусть Точка
принадлежит плоскости сечения и грани
как и точка
Тогда
где
— точка пересечения плоскости сечения с ребром
Далее имеем (
— общий,
как соответственные при
и секущей
).
Следовательно,
Рассмотрим и прямую
По теореме Менелая
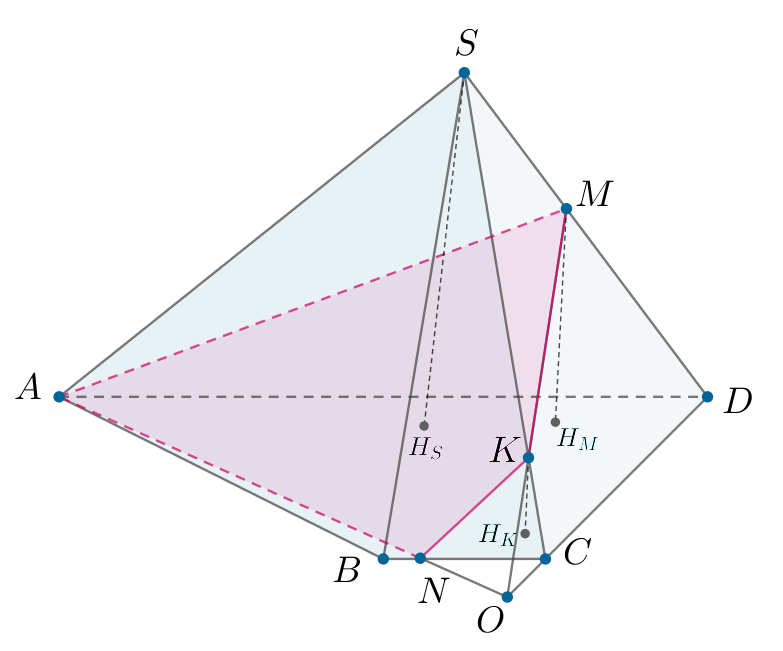
б) Докажем лемму: если — наклонная к плоскости
— точка на
то
Действительно,
так как
и эти прямые задают плоскость
Тогда как прямоугольные с общим углом
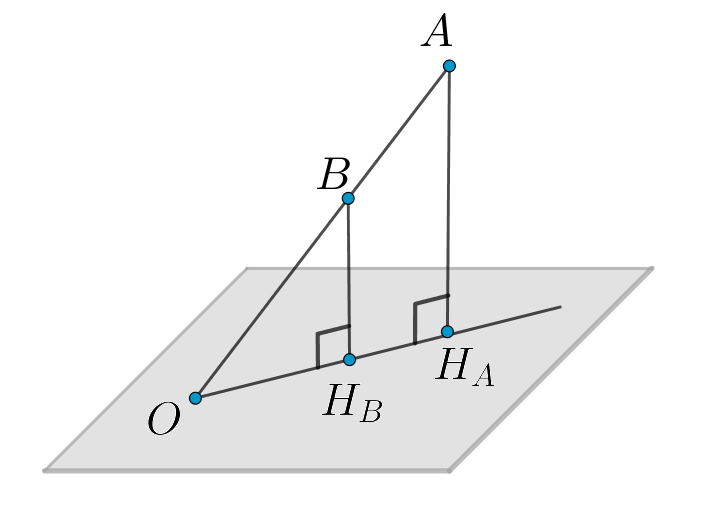
Проведем Тогда из подобий соответствующих пар треугольников следует, что
Найдем объем многогранника
как разность объемов треугольных пирамид
и
Рассмотрим основание Пусть
Тогда
следовательно,

Тогда
Окончательно имеем:
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Точка — середина ребра
правильной четырехугольной пирамиды
с основанием
Точка
принадлежит ребру
причем
a) Докажите, что плоскость параллельна прямой
б) Найдите площадь сечения пирамиды плоскостью если все ребра пирамиды равны 6.
Источники:
а) Назовем плоскость плоскостью
Пусть
— высота пирамиды, тогда
Пусть
Прямые
и
лежат в одной плоскости
следовательно, если требуется доказать, что
то нужно доказать, что
По теореме Менелая для и прямой
По теореме Менелая для и прямой
Следовательно, если то
значит,
и
Следовательно, по обратной теореме Фалеса
б) Если то четырехугольник
— сечение пирамиды плоскостью
Будем искать площадь сечения
через площадь проекции этого многоугольника на плоскость основания пирамиды и угол между плоскостями сечения и
основания.
Найдем — косинус угла между плоскостями
и
Проведем
тогда по ТТП
и
Ищем сначала
— прямоугольный (так как диагонали квадрата в основании правильной пирамиды взаимно перпендикулярны),
значит,
Тогда
Так как все ребра пирамиды равны, то Следовательно,
Так как
то
Следовательно,
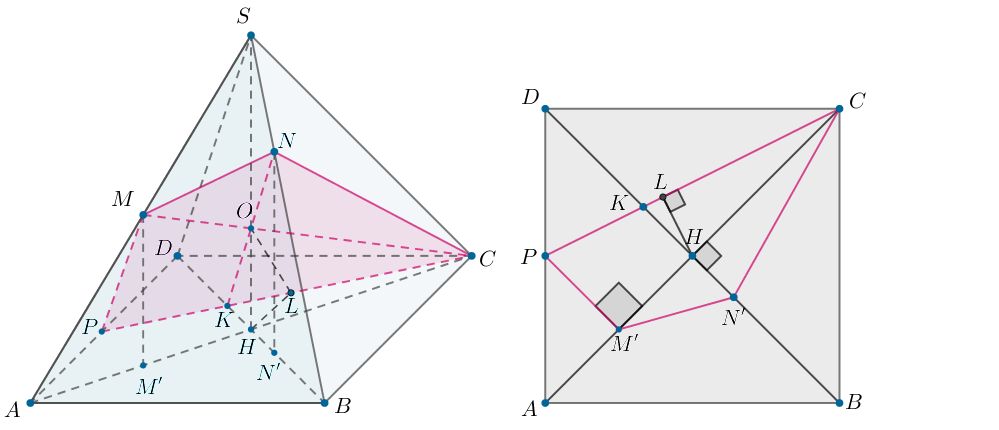
Теперь спроецируем на плоскость
Тогда
— проекция точки
и середина
— проекция
точки
причем
Получили четырехугольник
Так как то
следовательно,
— середина
Следовательно,
—
средняя линия в
значит,
Тогда
Так как то
следовательно,
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Дана четырехугольная пирамида Четырехугольник
— трапеция с большим основанием
отрезок
— ее средняя линия. Диагонали трапеции пересекаются в точке
Отрезок
содержится в плоскости
параллельной
а) Докажите, что сечение пирамиды плоскостью — трапеция.
б) Найдите площадь сечения пирамиды плоскостью если
а
Источники:
а) Пусть — точки пересечения
с диагоналями трапеции. Так как
то проведем
и получим
сечение пирамиды плоскостью
— четырехугольник
. Докажем, что это трапеция.
Так как лежит в
и
то
Следовательно,
пересечет плоскость, в которой лежит
по
прямой, параллельной
Следовательно,
Осталось доказать, что не параллельна
Действительно, так как
то
Тогда, так как
то
следовательно,
не параллельна
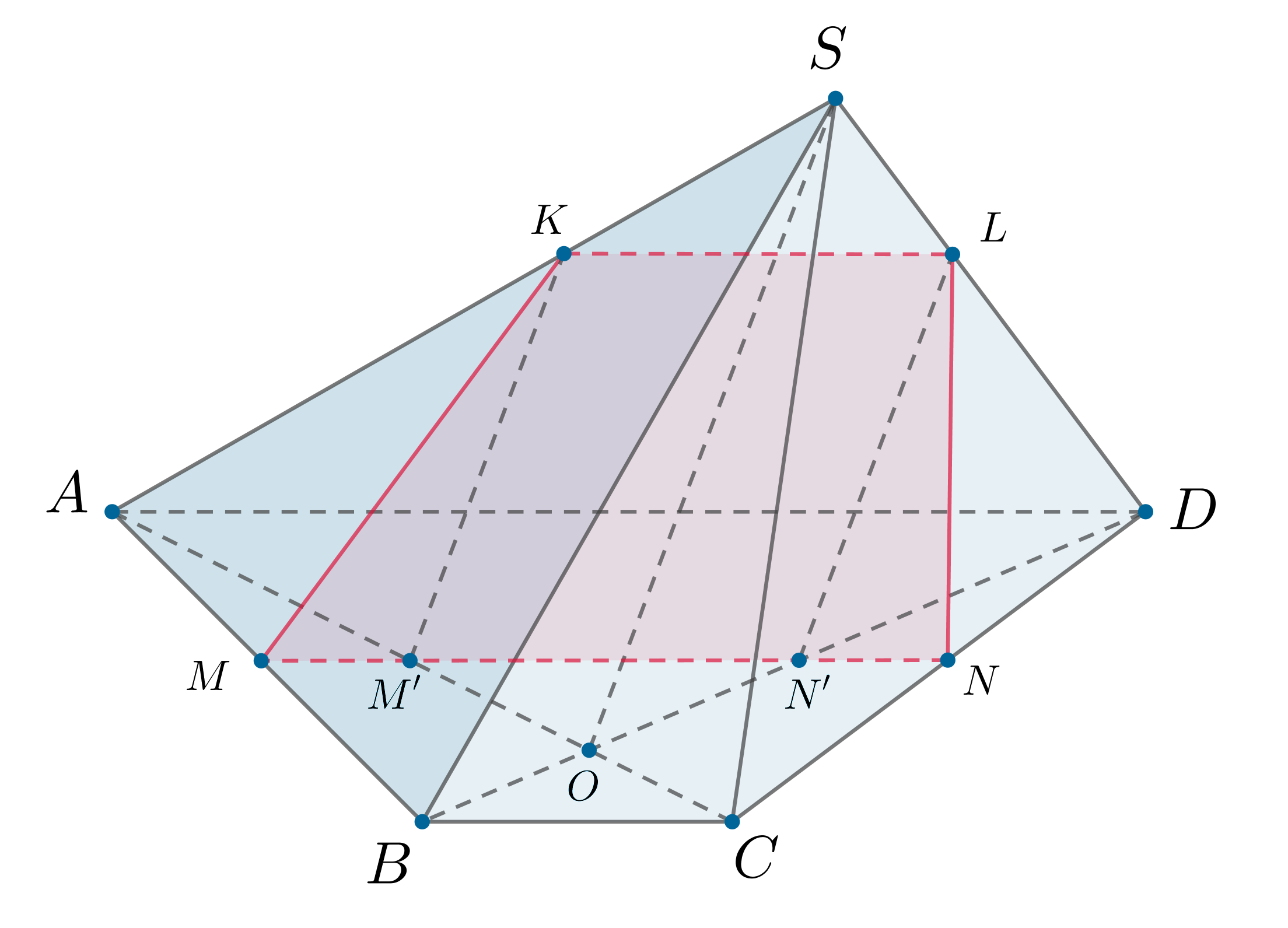
б) Так как то пусть
Тогда
Для точки имеем:
Из условия задачи следовательно, по теореме Фалеса
Значит а
Так как
то
следовательно,
— высота
трапеции, находящейся в сечении.
Тогда искомая площадь сечения равна
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Дана треугольная пирамида Основание высоты
этой пирамиды является серединой отрезка
— высоты
треугольника
а) Докажите, что
б) Найдите объём пирамиды если
Источники:
а) Заметим, что прямая проведённая через основание наклонной
в плоскости
перпендикулярна ее проекции
так как
— высота
Тогда по теореме о трех перпендикулярах
В прямоугольных треугольниках и
по теореме Пифагора:
Отсюда имеем:
![]()
Аналогично в прямоугольных треугольниках и
по теореме Пифагора:
Отсюда имеем:
б) Объем пирамиды можно вычислить по формуле
Найдем площадь треугольника
Пусть тогда
Из пункта а) имеем:
Отсюда получим
![]()
Тогда по теореме Пифагора для
Следовательно,
Найдем высоту пирамиды По условию
Так как
— высота пирамиды, то
—
прямоугольный и по теореме Пифагора:
Тогда искомый объем пирамиды равен
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
На окружности основания конуса с вершиной отмечены точки
и
так, что
— диаметр основания. Угол между
образующей и плоскостью основания равен
a) Докажите, что
б) Найдите объем тетраэдра если
и
Источники:
а) Пусть точка — центр основания конуса, то есть центр окружности основания. Тогда
— его высота, значит,
Следовательно, так как
— образующая конуса, то имеем:
Запишем теорему косинусов для треугольника
Запишем теорему косинусов для треугольника
![]()
Сложим два полученных равенства:
Рассмотрим треугольник В нем угол
равен
так как он опирается на диаметр
окружности основания.
Тогда по теореме Пифагора
Приравняем правые части и
б) По предыдущему пункту имеем:
Рассмотрим треугольник Он прямоугольный с углом
Тогда
Рассмотрим прямоугольный треугольник В нем
и
Тогда по теореме
Пифагора
![]()
Тогда можем найти объем
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Дан правильный треугольник и точка
не лежащая в плоскости треугольника и взятая таким образом, что
а) Докажите, что прямые и
перпендикулярны.
б) Найдите расстояние между прямыми и
если
Источники:
а) Так как то углы
и
равны.
Рассмотрим треугольники и
В них
— общая сторона,
так как
равносторонний и
Значит, треугольники
и
равны по первому признаку. В равных треугольниках соответственные
элементы равны, следовательно,
Пусть — середина
Тогда
— высота и медиана равностороннего треугольника
а
— высота и
медиана равнобедренного треугольника
Значит,
и
следовательно,
Прямая,
перпендикулярная плоскости, перпендикулярна каждой прямой, лежащей в этой плоскости, значит,
![]()
б) Пусть — высота треугольника
Тогда
так как
лежит в плоскости
и
Тогда
— общий перпендикуляр к прямым
и
то есть расстояние между данными прямыми есть длина отрезка
Запишем теорему косинусов для треугольника
Запишем теорему Пифагора для треугольника
По условию значит,
Тогда по теореме Пифагора для треугольника
Запишем теорему косинусов для треугольника
![]()
Подставим полученные значения
и
Рассмотрим треугольник Он прямоугольный, значит,
По теореме Пифагора для треугольника
Значит, расстояние между прямыми и
равно
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Дана треугольная призма Точка
— середина ребра
Плоскость
проходит через ребро
и
перпендикулярна прямой
а) Докажите, что одна из диагоналей грани равна одной из ее сторон.
б) Найдите расстояние от точки до плоскости
если
делит ребро
в отношении
считая от точки
и
а) По условию Если прямая перпендикулярна плоскости, то она перпендикулярна каждой прямой, лежащей в этой
плоскости, в частности,
Так как — призма, то
следовательно,
Рассмотрим треугольник в одноименной плоскости. Отрезок
является его медианой и высотой, значит,
— равнобедренный, то есть
Таким образом, в грани
диагональ
равна стороне
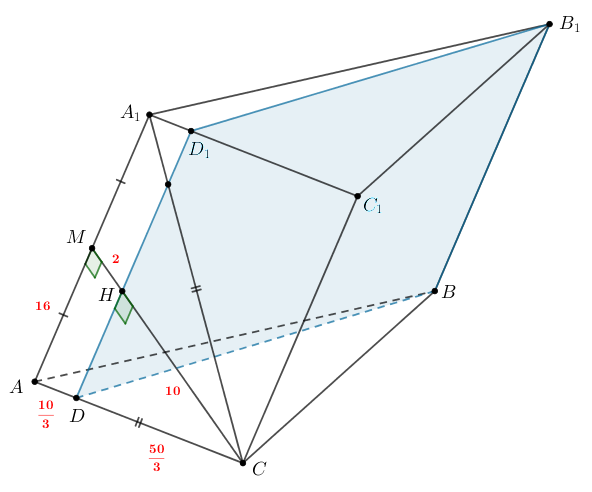
б) Пусть плоскость пересекает прямую
в точке
прямую
— в точке
, прямую
— в точке
Заметим, что все эти три точки лежат в грани
Значит, они лежат на прямой пересечения грани
плоскостью
Нам нужно найти расстояние от точки до плоскости
то есть длину
так как
а
— точка пересечения
и
По условию имеем:
Отсюда получаем
По условию значит,
Тогда

Рассмотрим треугольники и
Они подобны, так как
— общий и
как
соответственные углы, образованные параллельными прямыми
и
и секущей
Тогда имеем:
Найдем По условию
— середина
значит,
Треугольник — прямоугольный, тогда по теореме Пифагора:
Таким образом,
Отсюда Теперь можем найти длину
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
В основании пирамиды лежит трапеция
с большим основанием
Диагонали трапеции пересекаются в точке
Точки
и
— середины
боковых сторон
и
соответственно. Плоскость
проходит через точки
и
параллельно прямой
а) Докажите, что сечение пирамиды плоскостью
является
трапецией.
б) Найдите площадь сечения пирамиды плоскостью
если
а прямая
перпендикулярна прямой
Источники:
а) Пусть и
— точки пересечения прямой
с диагоналями
и
соответственно. Так как
то
пересечет плоскости, в которых лежит
по прямым, параллельным
Следовательно, плоскости
и
плоскость
пересечет по прямым
и
параллельным
Следовательно,
— сечение пирамиды плоскостью
Докажем, что
— трапеция.
Далее, так как
Следовательно,
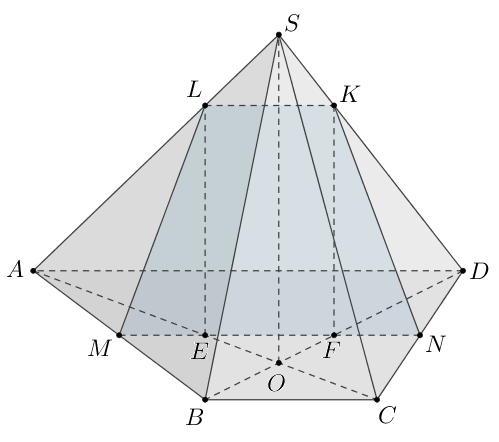
По теореме о пропорциональных отрезках имеем:
Следовательно, по обратной теореме о пропорциональных отрезках
Так как
как средняя линия, то
Так как
противоположные стороны четырехугольника
параллельны, то он
является параллелограммом. Следовательно,
Тогда две
стороны четырехугольника
не равны и параллельны, значит, это
трапеция.
б) Так как — средняя линия трапеции, то
Так как и
— средние линии в
и
соответственно,
параллельные
то имеем:
Следовательно,

Из следует, что
значит,
Так как
то
как прямоугольные по двум
катетам. Следовательно,
и сечение
— равнобедренная
трапеция, где
и
— ее высоты.
Из пункта а) следует, что
Следовательно, искомая площадь равна
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а) | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |


