.00 №17 из ЕГЭ 2024
Ошибка.
Попробуйте повторить позже
Пятиугольник вписан в окружность. Известно, что
а) Докажите, что
б) Найдите длину диагонали если
Источники:
а) Равные хорды и
стягивают равные дуги, следовательно, вписанные
углы, опирающиеся на них, равны, то есть
Тогда накрест
лежащие углы, образованные прямыми
и
и секущей
равны,
следовательно,
Равные хорды и
стягивают равные дуги, следовательно, вписанные
углы, опирающиеся на них, равны, то есть
Тогда накрест
лежащие углы, образованные прямыми
и
и секущей
равны,
следовательно,
Пусть — точка пересечения диагоналей
и
Тогда в
четырехугольнике
известно, что
и
значит,
— параллелограмм. Следовательно,
и
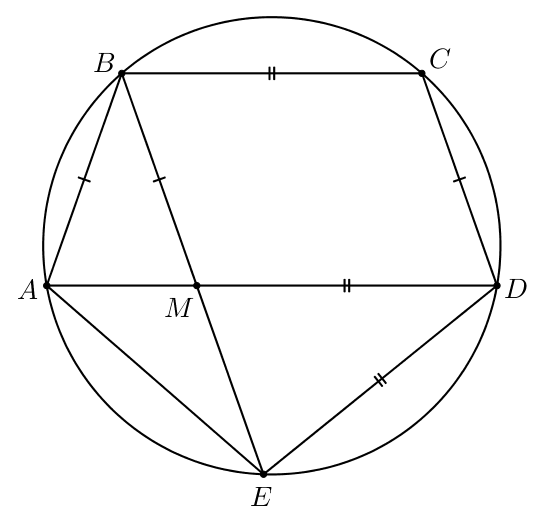
В четырехугольнике мы знаем, что
и
Значит,
—
равнобедренная трапеция. Диагонали равнобедренной трапеции равны, поэтому
В четырехугольнике мы знаем, что
и
Значит,
—
равнобедренная трапеция. Диагонали равнобедренной трапеции равны, поэтому
Таким образом,
б) В пункте а) мы узнали, что значит,
Тогда по свойству пересекающихся хорд и
в окружности:
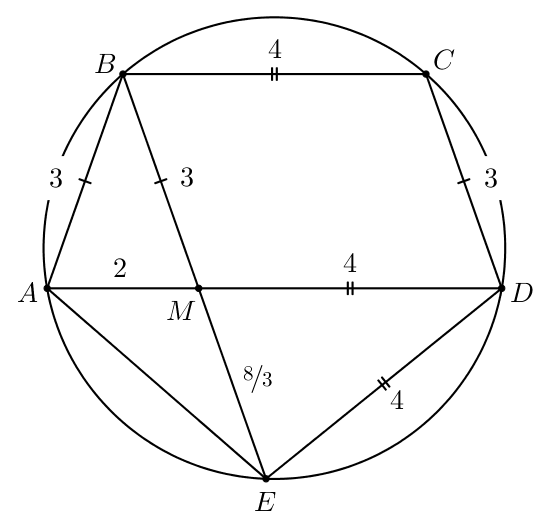
Значит,
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




