№17 из ЕГЭ 2023
Готовиться с нами - ЛЕГКО!
Ошибка.
Попробуйте повторить позже
Прямая, перпендикулярная стороне ромба
пересекает его диагональ
в точке
а диагональ
в точке
причем
а) Докажите, что
б) Найдите площадь ромба, если
а) Пусть прямая из условия пересекает в точке
а
— в точке
пусть
— точка пересечения диагоналей ромба. Опустим высоту
на
Заметим, что Тогда
Так как а
то
— середина
Запишем теорему Менелая для треугольника и прямой
По теореме о пропорциональных отрезках для угла и параллельных
прямых
и
(так как эти прямые перпендикулярны
) получаем
Таким образом, в два раза меньше
Значит,
Но в ромбе
тогда

б) Диагонали ромба делят его углы пополам, поэтому
Прямоугольные треугольники и
подобны по двум углам:
прямому и общему. Тогда
Значит, так как то по формуле двойного угла
Тогда
Значит,
Мы знаем, что
Тогда
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Дана равнобедренная трапеция с основаниями
и
Биссектрисы
углов
и
пересекаются в точке
Точки
и
отмечены на
боковых сторонах
и
соответственно. Известно, что
а) Докажите, что точки
и
лежат на одной прямой.
б) Найдите если известно, что
и
Источники:
а) Так как — биссектриса угла
то
По условию
значит, треугольник
— равнобедренный. Тогда
Таким образом,
Тогда накрест лежащие углы, образованные прямыми и
и секущей
равны. Значит,

Так как — биссектриса угла
то
По
условию
значит, треугольник
— равнобедренный. Тогда
Таким образом,
Тогда накрест лежащие углы, образованные прямыми и
и секущей
равны. Значит,
Тогда, так как — трапеция, то
Поскольку эти прямые
проходят через точку
то точки
и
лежат на одной прямой. Что и
требовалось доказать.
б) Заметим, что
Опустим из точки перпендикуляры
и
на прямые
и
соответственно. Тогда
Значит,
Тогда прямоугольные треугольники и
равны по гипотенузе и
острому углу, так как
и
Тогда
По пункту а) имеем и
Тогда по обобщенной теореме
Фалеса для прямых
и
и секущих
и

Найдем величину
Пусть — высота трапеции. Тогда
Пусть
Так как трапеция
— равнобедренная,
то
Заметим, что — прямоугольник, тогда
Значит,
получаем
Тогда имеем:
Следовательно,
Так как угол — острый, то получаем искомое отношение
б) 1 : 2
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Дана равнобедренная трапеция с основаниями
и
где
Биссектрисы углов
и
пересекаются в точке
Через
точку
провели прямую, параллельную основаниям, которая пересекла боковые
стороны
и
в точках
и
соответственно.
а) Докажите, что
б) Найдите если известно, что
и
Источники:
а) По условию Тогда
— трапеция. С другой стороны,
трапеция
— равнобедренная, тогда
Значит, — равнобедренная трапеция, то есть
Также из параллельности и
следует, что накрест лежащие углы
и
образованные секущей
равны. Значит,
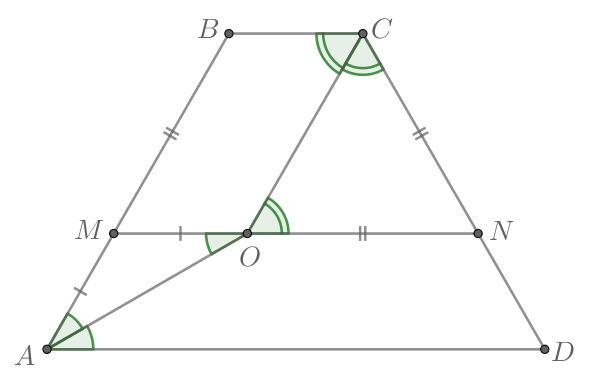
Таким образом, в треугольнике равны углы при стороне
Значит,
он равнобедренный и
Из параллельности и
следует, что накрест лежащие углы
и
образованные секущей
равны. Значит,
Таким образом, в треугольнике равны углы при стороне
Значит,
он равнобедренный и
Таким образом,
б) Заметим, что
Опустим из точки перпендикуляры
и
на
и
соответственно. Тогда
Значит,
Тогда прямоугольные треугольники и
равны по гипотенузе и
острому углу, так как
и
Тогда
По пункту а) и
Тогда по теореме Фалеса для прямых
и
и секущих
и
Значит, Таким образом,
Тогда
— большее
основание.
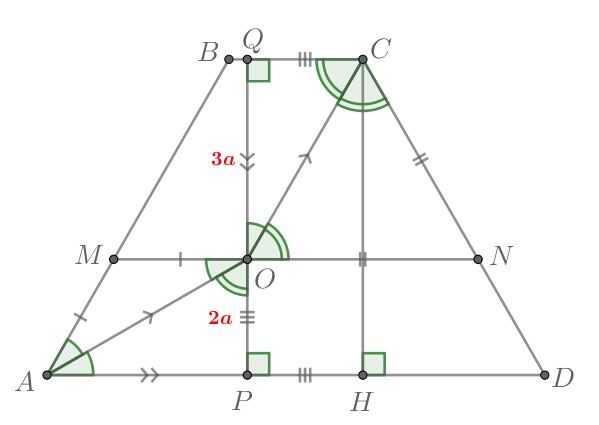
Найдем
Таким образом,
Пусть
Тогда
При этом
— высота трапеции. Пусть
— высота трапеции из
точки
Тогда
Из прямоугольного треугольника
Значит,
Заметим, что — прямоугольник, тогда
Значит,
Таким образом,
Так как трапеция — равнобедренная, то
Следовательно,
Тогда
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Дан равносторонний треугольник На его стороне
отмечена точка
Серединный перпендикуляр к отрезку
пересекает стороны
и
в
точках
и
соответственно.
а) Докажите, что угол равен углу
б) Найдите отношение площадей треугольников и
если
а) Треугольник — равносторонний, поэтому все его углы равны
Пусть Тогда
Точки
и
лежат на
серединном перпендикуляре к
поэтому
и
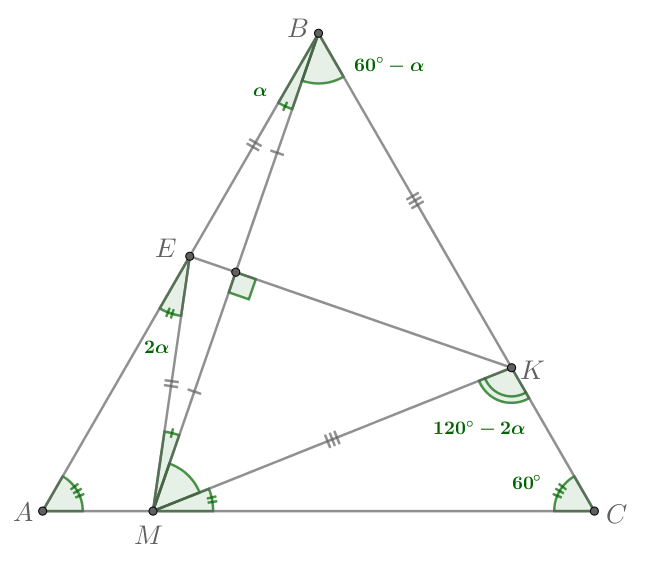
Таким образом, треугольники и
— равнобедренные. Тогда
Заметим, что — внешний для треугольника
поэтому
Аналогично — внешний для треугольника
поэтому
Тогда по сумме углов треугольника
б) Заметим, что треугольники и
подобны по двум углам, так
как
по пункту а),
Тогда
Пусть Тогда, так как
то получаем
Пусть Тогда
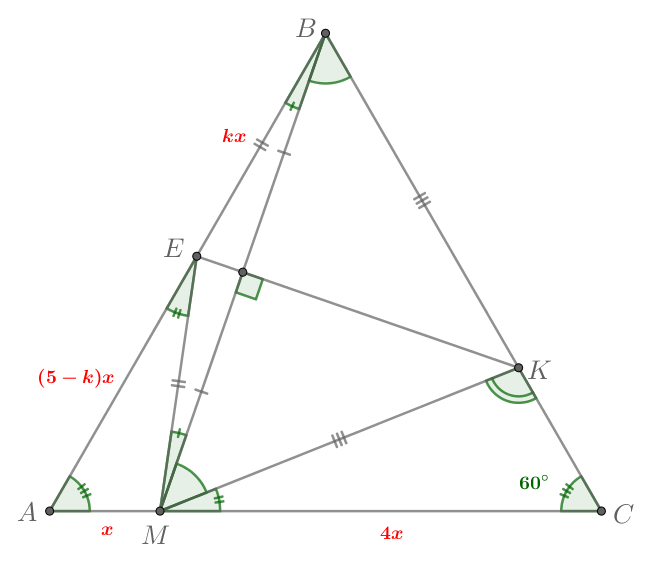
Запишем теорему косинусов для треугольника
Тогда а
Таким образом,
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
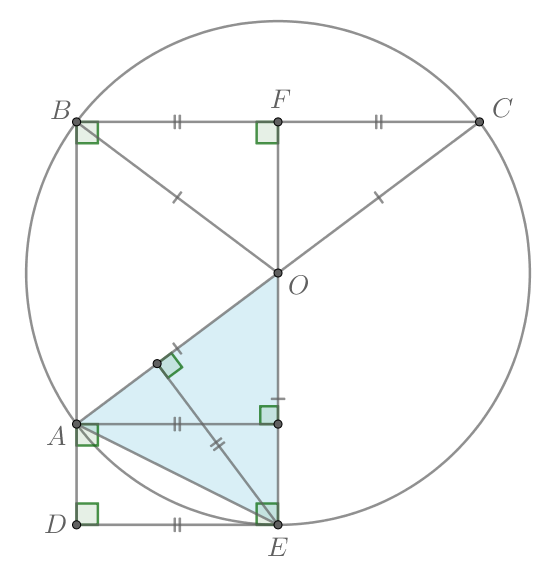
Прямая, перпендикулярная стороне ромба
пересекает его диагональ
в точке
а диагональ
— в точке
При этом
а) Докажите, что
б) Найдите площадь ромба, если
а) Пусть прямая из условия пересекает в точке
а
— в точке
Пусть
— точка пересечения диагоналей ромба. Опустим высоту
на
Заметим, что Тогда
Так как а
то
— середина
Запишем теорему Менелая для треугольника и прямой
Прямые и
перпендикулярны прямой
а значит параллельны.
Тогда по теореме Фалеса для угла
Таким образом, в два раза меньше
Значит,
Но в ромбе
тогда имеем:

б) Диагонали ромба делят его углы пополам, поэтому
Прямоугольные треугольники и
подобны по двум углам:
прямому и общему. Тогда имеем:
Значит, так как то по формуле косинуса двойного угла
Отсюда получаем
Значит,
Мы знаем, что
Тогда окончательно имеем:
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Прямая, перпендикулярная стороне ромба
пересекает его диагональ
в точке
а диагональ
в точке
причем
а) Докажите, что прямая делит сторону ромба
в отношении
б) Найдите сторону ромба, если
Источники:
а) Пусть прямая из условия пересекает в точке
а
— в точке
пусть
— точка пересечения диагоналей ромба. Опустим высоту
на
Заметим, что Тогда
Так как а
то
— середина
Запишем теорему Менелая для треугольника и прямой
По теореме Фалеса для угла и параллельных прямых
и
(обе
эти прямые перпендикулярны
)

Таким образом, в два раза меньше
Значит,
Значит,
Четырехугольник — прямоугольник. Тогда
следовательно,
б) Заметим, что
Диагонали ромба делят его углы пополам, поэтому
Прямоугольные треугольники и
подобны по двум углам:
прямому и общему. Тогда
Значит, так как то по формуле косинуса двойного угла
Тогда
Значит,
Пусть Тогда по теореме косинусов для треугольника
Таким образом, сторона ромба равна 6.
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Две окружности касаются внутренним образом в точке причем меньшая
проходит через центр большей. Хорда
большей окружности касается меньшей
в точке
Хорды
и
пересекают меньшую окружность в точках
и
соответственно.
a) Докажите, что прямые и
параллельны.
б) Пусть — точка пересечения отрезков
и
Найдите
если
радиус большей окружности равен 10, а
Источники:
а) Проведем через точку общую касательную
к окружностям.
Рассмотрим меньшую окружность. Мы знаем, что угол между хордой и
касательной к окружности равен половине дуги, заключенной между ними, значит,
угол между и
равен вписанному углу

Рассмотрим большую окружность. По аналогичным соображениям угол между
и
равен углу
Тогда, так как точки
и
лежат на одной прямой, то
Таким образом, по признаку параллельных прямых
б) Пусть и
— центры большей и меньшей окружностей соответственно.
Проведем радиус
Заметим, что
так как радиус,
проведенный в точку касания, перпендикулярен касательной.
Опустим перпендикуляр на
В равнобедренном треугольнике
отрезок
— высота, а значит и медиана. Тогда
По теореме Пифагора для треугольника

Так как отрезки и
— радиусы меньшей окружности, то
Рассмотрим прямоугольную трапецию
Пусть — перпендикуляр к
тогда
— прямоугольник
и
Следовательно, по теореме Пифагора
Тогда
Так как хорды данных окружностей, лежащие на одной прямой, проходящей
через точку относятся как их диаметры, то
— средняя линия в
треугольнике
Тогда
— средняя линия в треугольнике
и
— средняя линия в треугольнике
следовательно,
По теореме о произведении отрезков хорд имеем:
С учетом равенства получим
следовательно,
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Две окружности касаются внешним образом в точке Отрезки
и
—
диаметры первой и второй окружностей. Из точки
проведена касательная
ко второй окружности, которая вторично пересекает первую окружность в
точке
Луч
вторично пересекает первую окружность в точке
а) Докажите, что прямые и
параллельны.
б) Найдите площадь треугольника если
Источники:
а) Вписанный угол равен
так как опирается на диаметр
Вписанный угол
равен
так как опирается на диаметр
Таким
образом, накрест лежащие углы
и
образованные прямыми
и
и секущей
равны. Следовательно, прямые
и
параллельны.
б) Пусть — середина
Тогда
— центр окружности с диаметром
Проведем радиус
к точке касания. Получим, что
Рассмотрим треугольники и
Они подобны по двум углам:
— общий. Пусть
Запишем отношение
подобия:
Таким образом,

Из отношения подобия треугольников и
Рассмотрим прямоугольный треугольник В нем по теореме
Пифагора
Тогда
— трапеция,
и
— ее диагонали, а
— их точка
пересечения. Значит,
Тогда
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Две окружности касаются внутренним образом в точке причем меньшая
проходит через центр большей. Хорда
большей окружности касается
меньшей в точке
Хорды
и
пересекают меньшую окружность в
точках
и
соответственно, а отрезки
и
пересекаются в точке
a) Докажите, что
б) Найдите если
а радиус малой окружности равен
Источники:
а) Проведем через точку общую касательную
к окружностям.
Рассмотрим меньшую окружность. Мы знаем, что угол между хордой и
касательной к окружности равен половине дуги, заключенной между ними, значит,
угол между и
равен вписанному углу

Рассмотрим большую окружность. По аналогичным соображениям угол между
и
равен вписанному углу
Тогда, так как точки
и
лежат на одной прямой, то
Таким образом, по признаку параллельных прямых
Рассмотрим треугольники и
Они подобны по двум углам:
— общий, а
как соответственные при параллельных
прямых
и
и секущей
Запишем отношение подобия:
Рассмотрим треугольники и
Они подобны по двум углам:
— общий, а
как соответственные при параллельных
прямых
и
и секущей
Запишем отношение подобия:
Таким образом,
б) Пусть По условию
В предыдущем пункте мы
доказали, что
следовательно,
Тогда
Пусть и
— центры большей и меньшей окружностей соответственно.
Пусть
— перпендикуляр к
В равнобедренном треугольнике
отрезок
— это высота, а значит и медиана. Тогда
Таким
образом,

Заметим, что радиус большей окружности равен диаметру меньшей, то есть
Запишем теорему Пифагора для треугольника
Таким образом,
Проведем Так как касательная перпендикулярна радиусу, проведенному
в точку касания, то
Пусть — перпендикуляр к
Тогда
— прямоугольник,
следовательно,
Заметим, что
Тогда по теореме Пифагора для треугольника
Найдем
Таким образом,
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Окружность касается одной из сторон прямого угла в точке
и пересекает
другую сторону угла в точках
и
Точка
лежит на отрезке
а
— диаметр этой окружности.
a) Докажите, что
б) Найдите расстояние от точки до прямой
если
Источники:
а) Пусть — центр окружности. Продлим
до пересечения с
Пусть это
точка
Рассмотрим четырехугольник
В нем
так как
— радиус окружности, а
— касательная;
по условию.

Найдем угол Так как он вписанный, опирающийся на диаметр
то
Следовательно, — прямоугольник, то есть
Таким образом, — высота в равнобедренном треугольнике
а значит
и медиана. Имеем
Следовательно,
б) Расстояние от точки до прямой
равно высоте треугольника
проведенной из точки
к
Треугольник — равнобедренный, а значит высоты, проведенные к его
боковым сторонам, равны. Таким образом, расстояние от точки
до
прямой
равно высоте треугольника
проведенной из точки
к
Точка лежит на прямой
которая параллельна
следовательно,
расстояние от точки
до
равно расстоянию между параллельными
прямыми
и
а это и есть
Значит, расстояние от точки до
равно
По теореме о касательной и секущей имеем:
Следовательно, расстояние от точки до
равно 4.
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Дан треугольник Известно, что
На стороне
построен равносторонний треугольник
при этом точки
и
лежат по разные стороны от прямой
а) Докажите, что вокруг полученного четырехугольника можно
описать окружность.
б) Найдите расстояние от точки пересечения диагоналей четырехугольника
до центра его описанной окружности.
Источники:
а) Запишем теорему косинусов для треугольника
Так как то
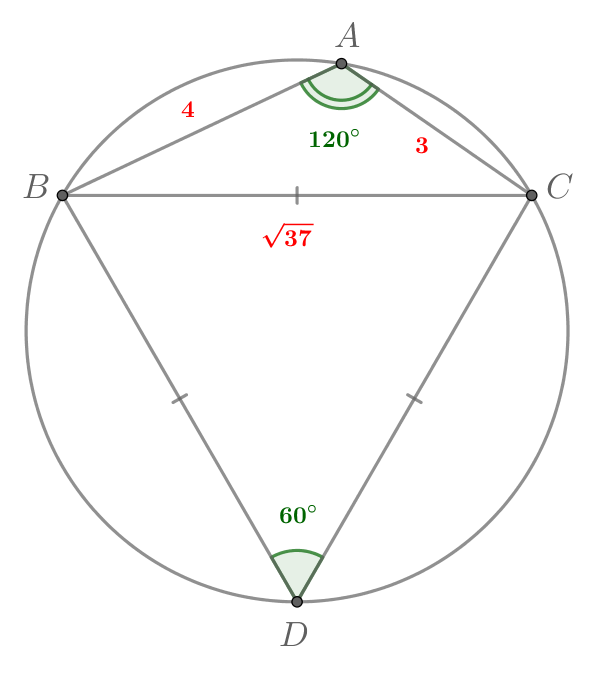
Тогда сумма противоположных углов четырехугольника равна
Значит, — вписанный четырехугольник.
б) Пусть — точка пересечения диагоналей
и
Заметим, что
— биссектриса угла
так как вписанные углы
и
опираются
на равные дуги. Тогда по свойству биссектрисы в треугольнике
имеем:
Значит, с учетом получаем
Пусть — центр описанной окружности
Тогда
— точка
пересечения медиан, высот и биссектрис равностороннего треугольника
Пусть
— одна из высот. Тогда имеем:

При этом — середина
то есть
Значит,
По теореме Пифагора для прямоугольного треугольника
Тогда искомое расстояние равно
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Дан треугольник Точки
и
отмечены на сторонах
и
соответственно, при этом
Точки
и
— середины
и
соответственно.
а) Докажите, что точки
и
лежат на одной окружности.
б) Найдите косинус угла, образованного отрезками и
если
Источники:
а) Проведем отрезки и
Рассмотрим треугольник
По условию
то есть он равнобедренный. Тогда его медиана
также является
высотой и биссектрисой. Значит,
Рассмотрим треугольник По условию
то есть он
равнобедренный. Тогда его медиана
также является высотой и биссектрисой.
Значит,

Таким образом, в четырехугольнике углы, опирающиеся на сторону
равны, следовательно,
— вписанный, то есть точки
и
лежат на одной окружности.
б) Пусть — точка пересечения
и
— точка пересечения
и
Тогда требуется найти модуль косинуса угла
Рассмотрим четырехугольник Он вписанный, так как сумма его
противоположных углов равна
Значит, по свойству вписанного четырехугольника
Углы и
равны как вертикальные.
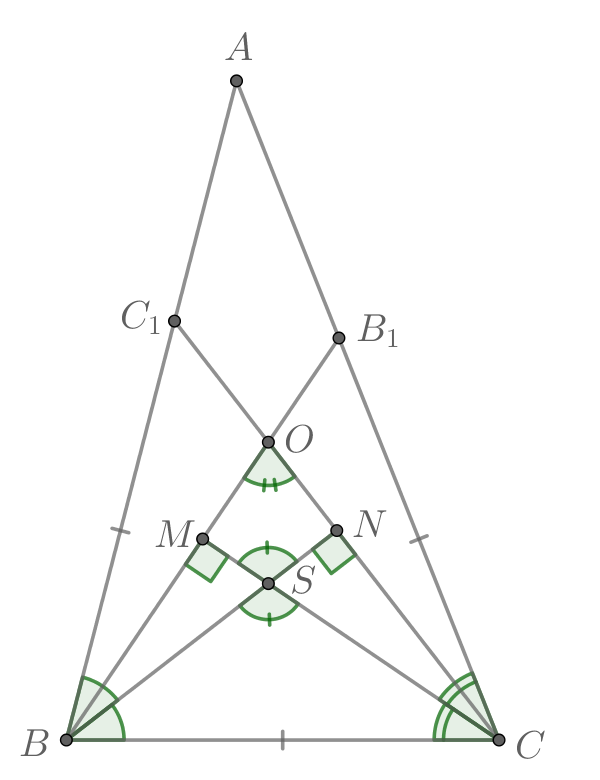
По сумме углов треугольника имеем
Таким образом,
Мы уже знаем, что и
— биссектрисы углов
и
треугольника
соответственно. Значит,
Так как сумма двух углов треугольника меньше то угол
острый
и модуль его косинуса равен его косинусу. Тогда далее будем искать косинус угла
Теперь проанализируем треугольник По условию в нем
Заметим, что
Значит, по теореме, обратной теореме Пифагора, — прямоугольный,
где
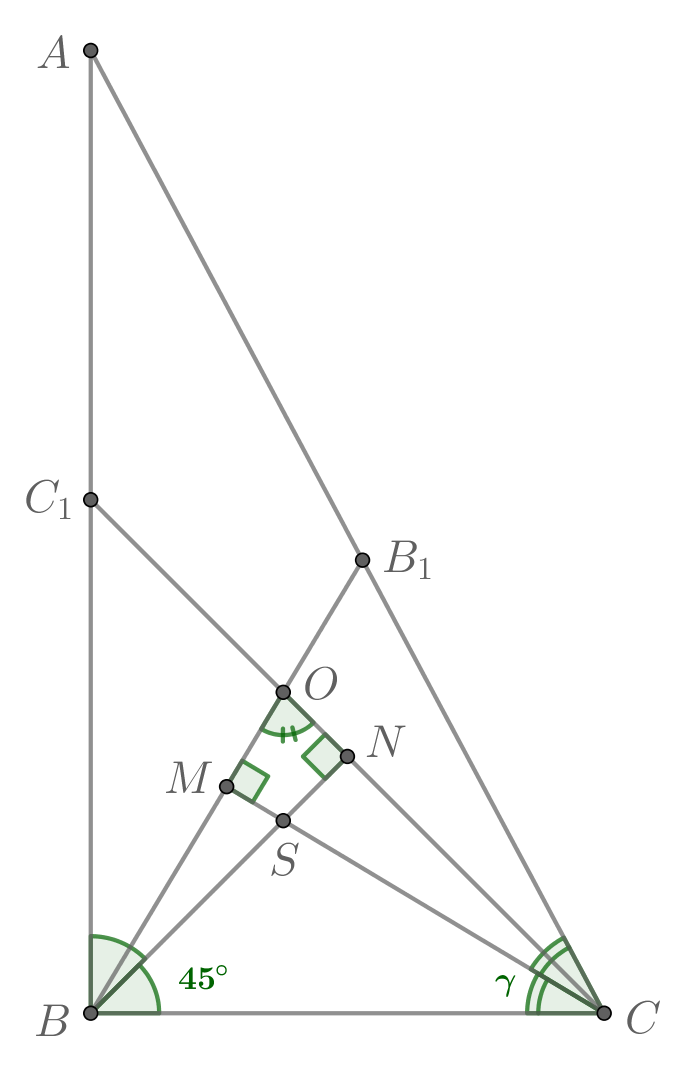
Пусть Тогда
Таким образом,
По формуле косинуса суммы
Треугольник — прямоугольный, значит,
Тогда
По основному тригонометрическому тождеству
Следовательно,
б)
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |
Ошибка.
Попробуйте повторить позже
Касательная к окружности, вписанной в квадрат пересекает его стороны
и
в точках
и
соответственно.
а) Докажите, что периметр треугольника равен стороне квадрата.
б) Прямая пересекает прямую
в точке
Через центр
вписанной окружности квадрата и точку
проведена прямая, которая
пересекает сторону
в точке
Известно, что
Найдите
Источники:
а) Пусть и
— середины сторон
и
Заметим, что
и
— точки
касания вписанной окружности и квадрата.

Пусть — точка касания вписанной окружности с прямой
Тогда отрезки касательных
и
проведенных из точек
к
вписанной окружности, равны, то есть
Аналогично
Тогда
б) Пусть — центр вписанной окружности,
— точка пересечения прямых
и
Рассмотрим треугольники и
В них углы
и
равны
как вертикальные, углы
и
равны как накрест лежащие,
образованные параллельными прямыми
и
и секущей
отрезки
и
равны, так как
— центр вписанной окружности квадрата, то есть и его
центр. Тогда по стороне и прилежащим к ней углам треугольники
и
равны.
Соответственные элементы равных треугольников равны, поэтому
Таким образом,
Заметим, что треугольники и
подобны по двум углам:
—
общий,
Тогда имеет место отношение
Пусть Тогда
то есть
Значит,
Следовательно,

Пусть Тогда
Таким образом,
Запишем теорему Пифагора для прямоугольного треугольника
В таком случае
Тогда
Заметим, что треугольники и
подобны по двум углам:
как вертикальные,
Запишем
отношение подобия:
Таким образом,
Тогда
Значит,
| Содержание критерия | Балл |
| Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б) | 3 |
| Обоснованно получен верный ответ в пункте б) | 2 |
| ИЛИ | |
| имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки | |
| Имеется верное доказательство утверждения пункта а), | 1 |
| ИЛИ | |
| при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, | |
| ИЛИ | |
| обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 3 |



