Полувписанные окружности
Ошибка.
Попробуйте повторить позже
В треугольнике 
точка 
— середина дуги 
содержащей точку 
описанной окружности 
— центр вписанной
окружности, 
— вторая точка пересечения прямой 
с 
— точка касания стороны 
с соответствующей вневписанной
окружностью, 
— вторая точка пересечения окружности 
с прямой, проходящей через 
и параллельной 
Докажите, что
прямые 
и 
пересекаются на окружности 
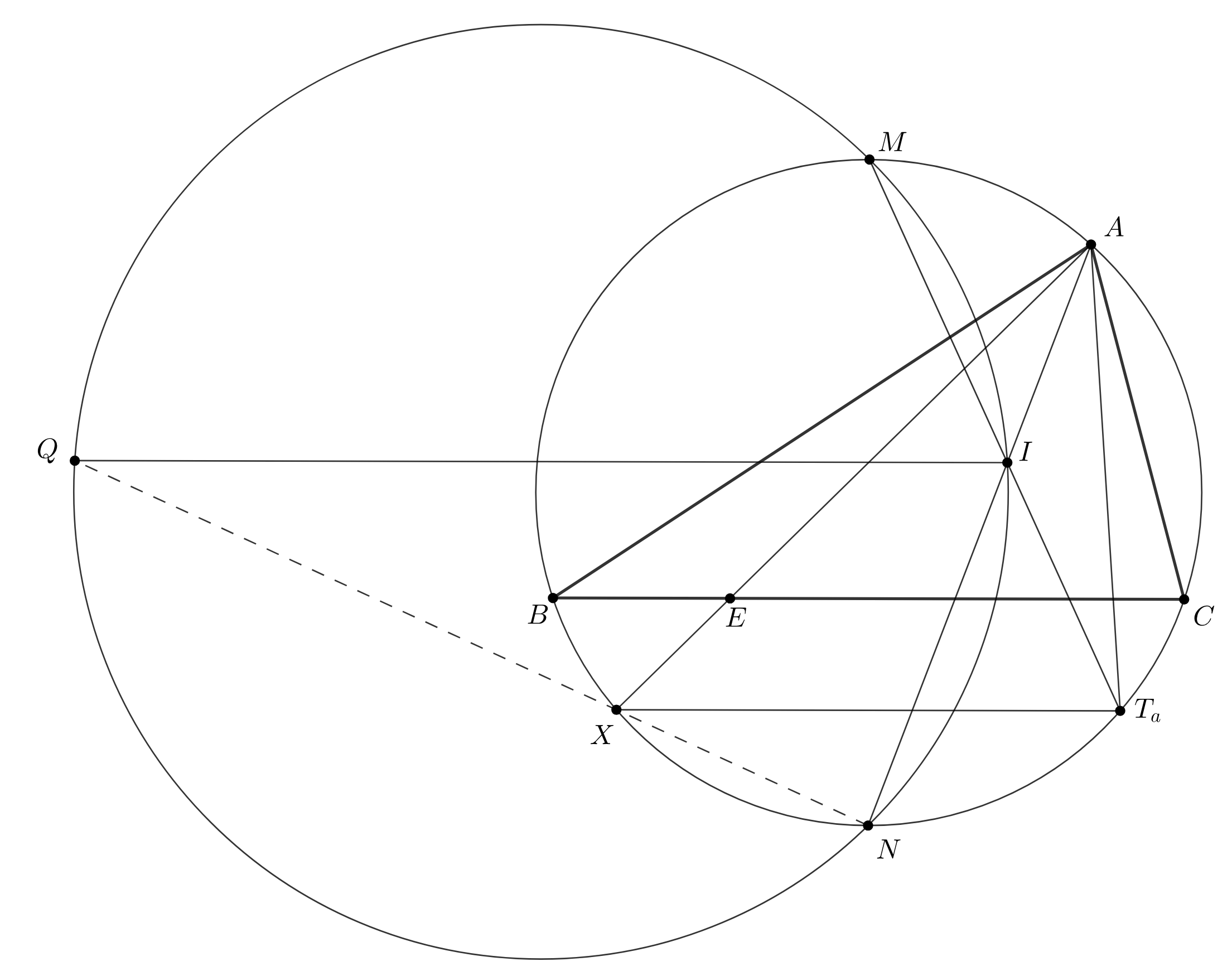
Обозначим полувписанную окружность как 
и пусть она касается “меньшей” дуги 
в точке 
Воспользуемся без доказательства
следующими фактами:
Лучи 
и 
симметричны относительно внутреннего угла 
Точки 
и 
лежат на одной прямой.
Пусть прямая 
вторично пересекает 
в точке 
. По свойству 1 прямые 
и 
параллельны. Поэтому прямые 
и 
также параллельны. По свойству 2 получаем, что
Следовательно, 
лежит на 
Специальные программы
Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!
Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.
Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.
Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».
Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!
Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!
