Тема Задачи №14 из ЕГЭ прошлых лет

№14 из ЕГЭ 2014

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#2315Максимум баллов за задание: 3

В правильной треугольной пирамиде $MABC$ с основанием $ABC$ стороны основания равны $6$ , а боковые ребра $8$ . На ребре $AC$ находится точка $D$ , на ребре $AB$ находится точка $E$ , а на ребре $AM$ – точка $L$ . Известно, что $CD = BE = LM = 2$ . Найдите площадь сечения пирамиды плоскостью, проходящей через точки $E$ , $D$ , $L$ .

Источники: ЕГЭ 2014, основная волна

Показать ответ и решение

Рассмотрим картинку:

$PIC$

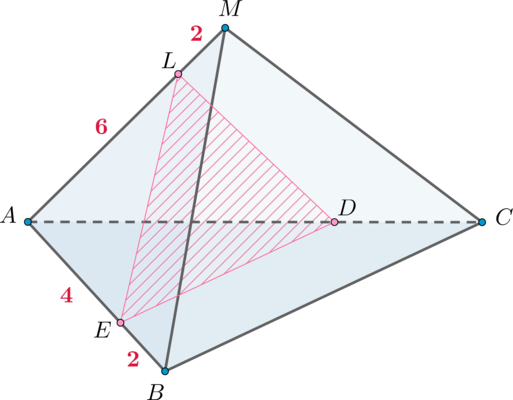
1) Заметим, что $△EDL$ есть сечение пирамиды плоскостью $EDL$ . Так как $BE = CD = 2$ и $AB = AC = 6$ , то $AE = AD = 4$ . Следовательно, $△AED ∼ △ABC$ по двум пропорциональным сторонам ( $AE : AB = AD : AC$ ) и углу между ними. Следовательно, $△AED$ тоже равносторонний, откуда $ED = AE = 4$ .

2) Заметим, что так как пирамида правильная, то $∠LAE = ∠LAD$ и $△LAE = △LAD$ . Следовательно, $LE = LD$ .

Рассмотрим грань $AM B$ . По теореме косинусов из $△AM B$ :

2 2 2 cos∠A = AM---+-AB---−--M-B---= 64-+-36-−-64-= 3- 2 ⋅ AM ⋅ AB 2 ⋅ 8 ⋅ 6 8

По теореме косинусов из $△LAE$ :

LE2 = AL2 + AE2 − 2 ⋅ AL ⋅ AE ⋅ cos ∠A = 36 + 16 − 2 ⋅ 6 ⋅ 4 ⋅ 3-= 34. 8

3) Рассмотрим $△EDL$ .

$PIC$

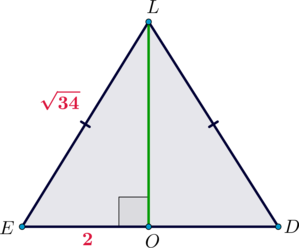
Он, как мы уже говорили, равнобедренный. Пусть $LO$ – высота, опущенная к основанию. Тогда

√ --- LO2 = LE2 − EO2 = 34 − 4 = 30 ⇒ LO = 30

Следовательно, площадь

1 √ --- S△EDL = --⋅ LO ⋅ ED = 2 30. 2

Ответ:

$√ --- 2 30$

Критерии оценки


Содержание критерия	Балл

Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б)	3

Обоснованно получен верный ответ в пункте б)	2
ИЛИ
имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки

Имеется верное доказательство утверждения пункта а)	1
ИЛИ
при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки
ИЛИ
обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	3

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#27471Максимум баллов за задание: 3

В правильной треугольной пирамиде $MABC$ с вершиной $M$ сторона основания $AB$ равна 6. На ребре $AB$ отмечена точка $K$ так, что $AK :KB = 5:1.$

a) Докажите, что объем пирамиды делится плоскостью $(MKC )$ в отношении $5:1.$

б) Сечение $MKC$ является равнобедренным треугольником с основанием $MK.$ Найдите угол между боковыми гранями пирамиды.

Источники: ЕГЭ 2014

Показать ответ и решение

а) Плоскость $(MKC )$ делит пирамиду $MABC$ на пирамиды $MAKC$ и $MBKC.$ Высоты данных пирамид совпадают с высотой пирамиды $MABC,$ пусть $h$ — ее длина. Тогда

1 1 VMAKC = 3 ⋅h ⋅SAKC, VMBKC = 3 ⋅h⋅SBKC

Следовательно,

1 VMAKC-= 3 ⋅h⋅SAKC-= SAKC- VMBKC 13 ⋅h⋅SBKC SBKC

$PIC$

Заметим, что треугольники $AKC$ и $BKC$ имеют общую высоту, проведенную из вершины $C,$ значит,

VMAKC-- SAKC- AK-- 5 VMBKC = SBKC = BK = 1

б) По условию $AK :KB = 5:1$ и $AB = 6,$ значит, $AK =5$ и $BK = 1.$ Запишем теорему косинусов для треугольника $CKB$ с углом $∠KBC = 60∘,$ так как $△ ABC$ — равносторонний:

CK2 = BC2 + BK2 − 2⋅BC ⋅BK cos∠KBC

Отсюда получаем

∘ --------------1 √-- CK = 36+ 1− 2⋅6⋅1⋅ 2 = 31

Тогда по условию $CM = CK = √31.$ Пусть $AN$ — высота треугольника $AMC.$

Рассмотрим треугольники $ANC$ и $BNC.$ В них $∠MCA = ∠MCB,$ так как пирамида $MABC$ правильная, $AB = BC$ и $CN$ — общая сторона. Тогда $△ ANC = △BNC.$ В равных треугольниках соответственные элементы равны, значит, $∘ ∠ANC = ∠BNC = 90 .$

$PIC$

Тогда исхомый угол между плоскостями равен углу $ANB.$ Из равенства треугольников $ANC$ и $BNC$ знаем, что $AN = BN.$

Найдем длину $BN.$ Для этого запишем теорему косинусов для треугольника $BMC :$

$BM2 = CM2 + BC2 − 2⋅CM ⋅BC cos∠NCB BC2 =2 ⋅CM ⋅BC cos∠NCB √ -- cos∠NCB = -BC--= 3--31- 2CM 31$

В прямоугольном треугольнике $BNC$ имеем:

CN 18√31- cos∠NCB = BC- ⇒ CN = BC cos∠NCB = -31--

Тогда по теореме Пифагора

∘---------- ∘ ----182 ∘ ----9- 6 √----- BN = BC2 − CN2 = 36− 31-= 6 1− 31 = 31 22⋅31

$PIC$

Теперь запишем теорему косинусов для треугольника $ANB :$

$AB2 = AN2 +BN2 − 2 ⋅AN ⋅BN cos∠ANB AB2 = 2AN2 − 2AN2 cos∠ANB cos∠ANB = 1− -AB2- 2AN2$

Подставим найденные ранее значения и найдем угол $ANB :$

36 31 13 13 cos∠ANB = 1− 2⋅36⋅ 22-= 1− 44 = 44 ⇒ ∠ANB = arccos44 31

Ответ:

б) $13 arccos44$

Критерии оценки


Содержание критерия	Балл

Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б)	3

Обоснованно получен верный ответ в пункте б)	2
ИЛИ
имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки

Имеется верное доказательство утверждения пункта а)	1
ИЛИ
при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки
ИЛИ
обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	3

Ошибка.
Попробуйте повторить позже

Задача 3#27472Максимум баллов за задание: 3

Радиус основания конуса с вершиной $P$ равен 6, а длина его образующей равна 9. На окружности основания конуса выбраны точки $A$ и $B,$ делящие окружность на две дуги, длины которых относятся как $1:3.$

a) Докажите, что угол $∠AP B$ меньше $60∘.$

б) Найдите площадь сечения конуса плоскостью $(ABP ).$

Источники: ЕГЭ 2014

Показать ответ и решение

а) Пусть $O$ — центр окружности основания. Тогда $AO = BO = 6.$ Рассмотрим меньшую дугу $AB.$ Ее длина составляет $1 4$ длины всей окружности, значит, $∠AOB = 90∘.$ Тогда в треугольнике $AOB :$

∘ ---------- √ ----- √ - √- AB = AO2 +BO2 = 2AO2 = AO 2= 6 2

Заметим, что $√ - √-- AB = 6 2= 72 <9,$ значит, в равнобедренном треугольнике $ABP$ сторона $AB$ является наименьшей и $∠AP B < 60∘.$

$PIC$

б) Сечением конуса плоскостью $(ABP )$ является треугольник $ABP.$ Пусть $M$ — середина $AB.$ Тогда $√- AM =BM = 3 2.$ Заметим, что так как $ABP$ — равнобедренный, то $PM$ является высотой и медианой треугольника $ABP.$ Тогда по теореме Пифагора для треугольника $AP M :$

PM = ∘AP--2−-AM2-= √81-− 18-= √63= 3√7

Теперь мы можем найти площадь треугольника $ABP :$

SABP = 1⋅PM ⋅AB = 1⋅3√7-⋅6√2= 9√14- 2 2

Ответ:

б) $√ -- 9 14$

Критерии оценки


Содержание критерия	Балл

Имеется верное доказательство утверждения пункта а) и обоснованно получен верный ответ в пункте б)	3

Обоснованно получен верный ответ в пункте б)	2
ИЛИ
имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки

Имеется верное доказательство утверждения пункта а)	1
ИЛИ
при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки
ИЛИ
обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	3