№15 из ЕГЭ 2016
Готовиться с нами - ЛЕГКО!
Ошибка.
Попробуйте повторить позже
Решите неравенство
Источники:
Найдем ОДЗ:
Заметим, что
При этом на ОДЗ выполнено
Тогда имеем:
Отсюда получаем
Пересечём ответ с ОДЗ и окончательно получим
Ошибка.
Попробуйте повторить позже
Решите неравенство
Источники:
Сделаем замену :
ОДЗ:
Перенесём всё влево и приведём к общему знаменателю
По методу интервалов
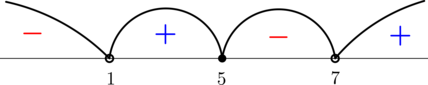
откуда
с учётом ОДЗ и условия :
в исходных переменных:
Ошибка.
Попробуйте повторить позже
Решите неравенство
Сделаем замену :
ОДЗ:
Перенесём всё влево и приведём к общему знаменателю
Разложим многочлен третьей степени в числителе левой части последнего неравенства на
множители. Можно угадать его корень . Знание корня многочлена позволяет поделить его
столбиком на
, где
– корень, тогда
По методу интервалов
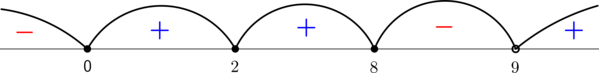
откуда
с учётом ОДЗ и условия :
в исходных переменных:
Ошибка.
Попробуйте повторить позже
Решите неравенство
Источники:
Найдем ОДЗ:
По методу рационализации на ОДЗ исходное неравенство равносильно неравенству
По методу интервалов имеем:

Отсюда с учётом ОДЗ окончательно получаем
| Содержание критерия | Балл |
| Обоснованно получен верный ответ | 2 |
| Обоснованно получен ответ, отличающийся от верного исключением/включением граничных точек, | 1 |
| ИЛИ | |
| получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения | |
| Решение не соответствует ни одному из критериев, перечисленных выше | 0 |
| Максимальный балл | 2 |
При этом в первом случае выставления 1 балла допускаются только ошибки
в строгости неравенства: «» вместо «
» или наоборот. Если в
ответ включено значение переменной, при котором одна из
частей неравенства не имеет смысла, то выставляется оценка «0
баллов».
Ошибка.
Попробуйте повторить позже
Решите неравенство
Источники:
Сделаем замену :
ОДЗ:
Перенесём всё влево и приведём к общему знаменателю
Разложим числитель левой части последнего неравенства на множители. Можно угадать его корень . Знание корня
многочлена позволяет поделить его столбиком на
, где
– корень, тогда
тогда последнее неравенство равносильно
По методу интервалов

откуда
с учётом ОДЗ и условия :
в исходных переменных:
Ошибка.
Попробуйте повторить позже
Решите неравенство
Источники:
Сделаем замену :
ОДЗ:
Перенесём всё влево и приведём к общему знаменателю
По методу интервалов
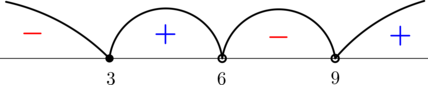
откуда
с учётом ОДЗ и условия :
в исходных переменных:

