Тема Задачи №16 из ЕГЭ прошлых лет

№16 из ЕГЭ 2017

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#1093Максимум баллов за задание: 2

В июле планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:
— каждый январь долг возрастает на $r%$ по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплачивать часть долга.
Найдите $r$ , если известно, что если ежегодно выплачивать по $777600$ рублей, то кредит будет погашен за 4 года, а если ежегодно выплачивать по $1 317600$ рублей, то кредит будет полностью погашен за 2 года.

Источники: ЕГЭ 2017, основная волна

Показать ответ и решение

Пусть $A$ рублей – сумма, взятая в кредит. Заметим, что кредит будет выплачиваться аннуитетными платежами. Обозначим за $t = 1010+0r0-$ , $x = 777600$ и $y = 1317600$ и составим таблицу для обоих случаев (когда кредит выплачивался 4 года и 2 года):

------------------------------------------------------------------------------ |Н ом ер года |Д олг до начи сления % |Д олг посл е н ачислен ия % |Пл атеж | |-------------|------------------------|----------------------------|---------| |1------------|A-----------------------|tA--------------------------|---x-----| |2------------|tA-−-x------------------|t(tA-−-x)-------------------|---x-----| |3------------|t(tA--−-x)-−-x-----------|t(t(tA--−-x) −-x)------------|---x-----| |4 |t(t(tA − x) − x) − x |t(t(t(tA − x) − x ) − x ) | x | ------------------------------------------------------------------------------

Тогда после последнего платежа долг будет равен

2 t(t(t(tA − x) − x) − x) − x = 0 ⇔ t4A = x(t3 + t2 + t + 1) ⇒ A = x(t-+-1)(t-+-1)- (∗ ) t4

|-------------|------------------------|----------------------------|---------| |Н-ом-ер-года-|Д-олг-до-начи-сления-%--|Д-олг-посл-е н-ачислен-ия-%-|Пл-атеж--| |1 |A |tA | y | |2------------|tA-−-y------------------|t(tA-−-y)-------------------|---y-----| ------------------------------------------------------------------------------|

Тогда после последнего платежа долг будет равен

t(tA − y) − y = 0 ⇔ t2A = y (t + 1) ⇒ A = y(t +-1) (∗∗) t2

Приравняем правые части уравнений $(∗ )$ и $(∗∗)$ :

x (t + 1)(t2 + 1) y(t + 1 ) x(t2 + 1) -------t4-------= ---t2--- ⇒ ---t2----= y

Сделаем подстановку и найдем $t$ :

x 777600 7776 t2 = ------= ------------------ = ----- = 1,44 y − x 1317600 − 777600 5400

Тогда

∘ ----- t = 1,44 = 1,2 ⇒ r = 20.

Ответ: 20

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#1110Максимум баллов за задание: 2

В июле планируется взять кредит в банке на сумму $7$ млн. рублей на некоторых срок (целое число лет). Условия его возврата таковы:
— каждый январь долг возрастает на $20%$ по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплачивать часть долга;
— в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
На сколько лет взят кредит, если известно, что общая сумма выплат после его погашения равнялась $17,5$ млн. рублей?

Источники: ЕГЭ 2017, основная волна

Показать ответ и решение

Так как выплачивается кредит дифференцированными платежами, то если $n$ – количество лет, на которое взят кредит в $7$ млн. рублей, значит, каждый год после платежа долг должен уменьшаться на $-7 n$ млн. рублей. Значит, в последний, $n$ -ый год, долг будет равен $7 n$ млн. рублей. Платеж, как и обычно в дифференцированных платежах, состоит из процентов, набежавших на сумму долга в этот год, плюс $7 n$ млн. рублей.
Составим таблицу:

|----|------------------------|----------------------------|----------------| |Год-|Д-олг-до-нач-ислени-я-%-|-Дол-г п-осле-начисл-ения-%-|----Пл-атеж-----| |1 | 7 | 7 + 0,2 ⋅ 7 | 0,2 ⋅ 7 + 7 | |2---|---------7-−-7----------|----7-−-7-+-0,2-(7-−-7)-----|0,2-(7 −-7)-n+-7-| |----|-------------n----------|--------n------------n------|---------n----n-| |...--|-----------...-----------|-------------...-------------|-------...-------| -n---------------7n----------------------7n +-0,2 ⋅-7n-----------0,2-⋅n7+--7n----

Тогда переплата по кредиту равна сумме первых слагаемых из столбца “Платеж”:

( 7) 7 ( ( 7) 7) 0,2 ⋅ 7 + 0,2 ⋅ 7 −-- + ⋅⋅⋅ + 0,2 ⋅--= 0,2 ⋅ 7 + 7 − -- + ⋅⋅⋅ +-- = n n n n

Заметим, что в скобках находится сумма арифметической прогрессии, где первый член равен $7$ , разность равна $− 7 n$ , последний член равен $7 n$ , а всего членов $n$ штук. Следовательно,

7 + 7 = 0,2 ⋅----n-⋅ n = 0, 7(n + 1) 2

Это мы вычислили переплату по кредиту. С другой стороны, если общая сумма выплат после погашения кредита составила $17,5$ млн. рублей, а в кредит было взято $7$ млн. рублей, то переплата равна $10, 5$ млн. рублей. Следовательно,

0,7(n + 1) = 10,5 ⇒ n = 14

Ответ: 14

Ошибка.
Попробуйте повторить позже

Задача 3#2429Максимум баллов за задание: 2

В июле 2020 года планируется брать кредит в банке на некоторую сумму. Условия его возврата таковы:
— каждый январь долг возрастает на $30%$ по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплачивать одним платежом часть долга.
Сколько рублей было взято в банке, если известно, что кредит был полностью погашен тремя равными платежами (то есть за 3 года) и сумма платежей превосходит взятую в банке сумму на $156060$ рублей?

Источники: ЕГЭ 2017, основная волна

Показать ответ и решение

Пусть $A$ рублей – сумма, взятая в кредит. Заметим, что кредит будет выплачиваться аннуитетными платежами. Обозначим за $t = 1,3$ и составим таблицу:

|-------------|------------------------|----------------------------|---------| |Н ом ер года |Д олг до начи сления % |Д олг посл е н ачислен ия % |Пл атеж | |1------------|A-----------------------|tA--------------------------|---x-----| |-------------|------------------------|----------------------------|---------| |2------------|tA-−-x------------------|t(tA-−-x)-------------------|---x-----| -3-------------t(tA--−-x)-−-x------------t(t(tA--−-x) −-x)----------------x-----|

Тогда после последнего платежа долг будет равен

At3 t(t(tA − x ) − x ) − x = 0 ⇔ t3A = x(t2 + t + 1) ⇒ x = -2-------- t + t + 1

По условию $3x − A = 156060$ , следовательно,

3 --3At----− A = 156060 ⇒ 3⋅2, 197A − 3, 99A = 156060 ⋅3,99 ⇒ A = 156060-⋅ 3990 = 60⋅3990 = 239400 t2 + t + 1 2601

Ответ: 239400

Ошибка.
Попробуйте повторить позже

Задача 4#2450Максимум баллов за задание: 2

15 января планируется взять кредит в банке на 15 месяцев. Условия его возврата таковы:

— 1 числа каждого месяца долг возрастает на $r%$ по сравнению с долгом на конец предыдущего месяца;

— со 2 по 14 число каждого месяца необходимо выплачивать часть долга;

— 15 числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15 число предыдущего месяца.

Найдите $r,$ если известно, что общая сумма выплат после полного погашения кредита на 120% больше суммы, взятой в кредит.

Источники: ЕГЭ 2017, основная волна

Показать ответ и решение

Пусть $A$ рублей — сумма, взятая в кредит. Обозначим $0,01r = y$ и составим таблицу. Из условия следует, что кредит будет выплачиваться дифференцированными платежами.

|------|--------------------|---------------------|---------------| |М-есяц-|Д-олг-до начисления %|Долг после начисления-%----Платеж-----| |1-----|---------A----------|------A-+-y⋅A--------|---y-⋅A-+-A15----| |2 | A− -A | A− -A+ y⋅(A − A) |y ⋅(A − A-)+ A- | |------|----------15--------|-----15---------15---|-------15---15-| |... | ... | ... | ... | |------|---------A----------|------A------A-------|------A---A----| -15--------------15-----------------15 +-y⋅15----------y⋅15 +-15---|

Заметим, что сумма первых слагаемых из последнего столбца и есть переплата по кредиту. Так как общая сумма выплат по кредиту превышает сумму кредита на 120%, то это значит, что переплата составляет 120% от кредита. Тогда получаем уравнение:

( ) y ⋅A + y⋅ A − A- + ...+ y⋅ A = 1,2A ⇔ ( 1(5 ) 15 ) 1- 1- ⇔ y ⋅A⋅ 1 + 1− 15 +...+ 15 = 1,2A

Заметим, что в скобках находится сумма арифметической прогрессии, где $a1 = 1,$ $-1 a15 = 15.$ Следовательно,

y ⋅A ⋅ 1-+115 ⋅15= 1,2A ⇔ 8y = 1,2 ⇔ y = 0,15 2

Отсюда найдем $r :$

r = 100y = 15

Ответ: 15

Критерии оценки


Содержание критерия	Балл

Обоснованно получен верный ответ	2

Верно построена математическая модель	1

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	2

Подробнее: 1 балл выставляется в тех случаях, когда сюжетное условие задачи верно сведено к решению математической (арифметической, алгебраической, функциональной, геометрической) задачи, но именно к решению, а не к отдельному равенству, набору уравнений, уравнению, задающему функцию, и т.п. Предъявленный текст должен включать описание того, как построена модель.

Ошибка.
Попробуйте повторить позже

Задача 5#2456Максимум баллов за задание: 2

15 января планируется взять кредит в банке на сумму 9 млн. рублей на некоторое целое число месяцев. Условия его возврата таковы:

– 1 числа каждого месяца долг возрастает на 20% по сравнению с долгом на конец предыдущего месяца;

– со 2 по 14 число каждого месяца необходимо выплачивать часть долга;

– 15 числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15 число предыдущего месяца.

Чему будет равна общая сумма выплат после полного погашения кредита, если наибольший платеж составит 3,6 млн. рублей?

Источники: ЕГЭ 2017, основная волна

Показать ответ и решение

Из условия следует, что система платежей дифференцированная. Исходя из этого составим таблицу следующим образом:

|------|--------------------|---------------------|--------------| |М-есяц-|Д-олг до начисления %|Долг после начисления-%---Платеж----| |1-----|---------9----------|------9-+0,2⋅9-------|---0,2-⋅9+-9n---| |2 | 9 − 9 | 9− 9 + 0,2⋅(9− 9) |0,2⋅(9− 9)+ 9 | |------|-----------n--------|-----n----------n----|--------n---n-| |... | ... | ... | ... | |------|---------9----------|------9------9-------|-------9--9---| -n---------------n-----------------n-+0,2⋅n-----------0,2⋅-n +-n---

Тогда общая сумма выплат после погашения равна сумме всех платежей:

( ) ( ) 0,2⋅ 9 +9 − 9+ ⋅⋅⋅+ 9- +n ⋅ 9-= 0,2⋅ 9 +9 − 9+ ⋅⋅⋅+ 9 +9 n n n n n

Заметим, что при дифференцированной системе платежей наибольший платеж – это первый платеж. Следовательно,

9 0,2⋅9+ n-= 3,6 ⇒ n = 5

Таким образом, общая сумма выплат равна

( ( 9) ( 9) ( 9 ) 9) ( 9) 0,2⋅ 9 + 9− 5 + 9− 2⋅5 + 9− 3⋅5 + 5 + 9= 0,2 ⋅ 9⋅4− 5⋅5 + 9= 14,4

Ответ: 14,4 млн. рублей

Критерии оценки


Содержание критерия	Балл

Обоснованно получен верный ответ	2

Верно построена математическая модель	1

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	2

Ошибка.
Попробуйте повторить позже

Задача 6#1014Максимум баллов за задание: 2

Страховой фонд владеет акциями, стоимость которых равна $t2$ тыс. рублей в конце каждого года с номером $t,$ где $t= 1;2;...$ Фонд может продать все акции в конце некоторого года и положить все вырученные с продажи средства на счет в банке. Известно, что тогда в конце каждого следующего года банк будет увеличивать сумму, находящую на счете, в $r$ раз, где $r$ — некоторое положительное большее единицы число. Оказалось, что если фонд продаст все акции и вложит деньги в банк именно в конце 21-ого года, то в конце 25-ого года он получит наибольшую из возможных прибыль. Определите, какие при этом значения может принимать число $r.$

Источники: ЕГЭ 2017, досрочная волна

Показать ответ и решение

Если фонд продаст акции в конце $t$ -ого года, то на конец 25-ого года они пролежат в банке $25− t$ лет. Так как каждый год банк увеличивает сумму в $r$ раз, то за $25 − t$ лет он увеличит ее в $r25−t$ раз. Следовательно, на конец 25-ого года фонд будет иметь сумму в тыс. рублей, равную

2 25−t f(t)= t ⋅r

Рассмотрим эту функцию. В ней $r$ — некоторое конкретное, но неизвестное число, а $t$ — переменная. Найдем ее производную:

′ 25−t 2 25−t 25−t f = 2t⋅r + t ⋅r ⋅ln r⋅(− 1)= r ⋅t⋅(2 − tlnr)

Таким образом, нулем производной, учитывая, что $t≥ 1,$ является $t= -2-. lnr$

Причем заметим, что эта точка является точкой максимума. Следовательно, до $2 t= ln-r$ функция возрастает, а после — убывает.

Таким образом, если, продав акции в 21-ый год, фонд получит наибольшую из возможных прибыль, то это значит, что мы имеем такой график:

$PIC$

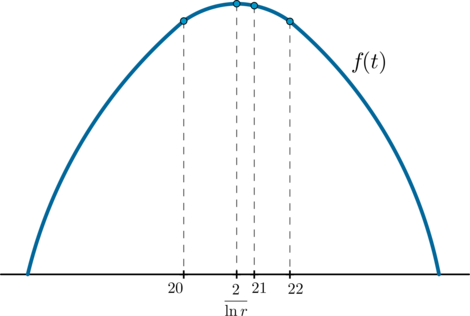
Для примера на картинке точка $t= 21$ находится правее точки максимума. Может быть наоборот: 21 будет находиться левее точки максимума. Главное, что точка графика с абсциссой 21 выше, чем точки графика с абсциссами 20 или 22!

Тогда $f(21)> f(20)$ и $f(21)> f(22).$ Из этого условия будет следовать, что $f(21)> f(t)$ при любом целом $t$ от 1 до 25. Решим полученную систему:

( 212 {212⋅r4 > 202⋅r5 ||{ r < 202 212⋅r4 > 222⋅r3 ⇒ | 2 |( r > 22212

Отсюда получаем, что $( ) r ∈ 484; 441 . 441 400$

Ответ:

$( 484 441-) r ∈ 441;400$

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#1097Максимум баллов за задание: 2

В июне 2020 года планируется взять кредит в банке на 3 года в размере $A$ млн. рублей, где $A$ — целое число. Условия его возврата таковы:

— каждый январь банк увеличивает сумму долга на 20% по сравнению с концом предыдущего года;

— с февраля по май необходимо выплатить часть долга одним платежом;

— в июне каждого года долг должен составлять часть кредита в соответствии со следующей таблицей:

|---М-есяц и-год----|июнь-2020-|ию-нь 2021|июнь 2022|июнь-2023-| |Долг (в м-лн. рублей)---A----|---0,8A----|--0,4A----|---0-----| -------------------------------------------------------------

Найдите наибольшее значение $A,$ при котором каждый платеж будет менее 5 млн. рублей.

Источники: ЕГЭ 2017, досрочная волна, резерв

Показать ответ и решение

Составим таблицу:

|-----|-----|--------------|------------------| |-год--|июнь-|---январь-----|-----платеж-------| |2020-|-A---|---A+-0,2A-----|-x1-=-0,2A+-0,2A----| |2021-|0,8A--|0,8A-+-0,2⋅0,8A--|x2 =-0,2⋅0,8A+-0,4A-| |22002223-|0,40A--|0,4A-+-0,2⋅0,4A--|x3 =-0,2⋅0,4A+-0,4A-| ----------------------------------------------

По условию

( |{x1 =0,4A< 5 -5-- 52 |(x2 =0,56A< 5 ⇒ A < 0,56 = 856 x3 =0,48A< 5

Следовательно, наибольшее целое $A = 8.$

Ответ: 8

Ошибка.
Попробуйте повторить позже

Задача 8#2453Максимум баллов за задание: 2

В июле планируется взять кредит в банке на сумму 8 млн. рублей на срок 10 лет. Условия его возврата таковы:

— каждый январь долг возрастает на $r%$ по сравнению с долгом на конец предыдущего года;

— с февраля по июнь необходимо выплатить часть долга так, чтобы на начало июля каждого года долг уменьшался на одну и ту же сумму по сравнению с предыдущим июлем.

Найдите наименьшую возможную ставку $r,$ если известно, что последний платеж будет не менее 0,92 млн. рублей.

Источники: ЕГЭ 2017, официальный пробный 21.04.2017

Показать ответ и решение

Фраза «на начало июля каждого года долг уменьшается на одну и ту же сумму по сравнению с предыдущим июлем» означает, что кредит выплачивается дифференцированными платежами.

Составим таблицу (ведя вычисления в млн. рублей), обозначив величину $r 100 = 0,01r = t:$

|----|--------------------|---------------------|-------------| |Год-|Д-олг до начисления %|Долг после начисления-%|П-латеж-----| |1 | 8 | 8+ t⋅8 | 110-⋅8+ t⋅8 | |----|--------9-----------|-----9-------9-------|-1-------9---| |2---|--------10-⋅8--------|----10 ⋅8+-t⋅10 ⋅8---|-10-⋅8+-t⋅10-⋅8| |... | ... | ... |... | |----|--------1-----------|-----1-------1-------|-1-------1---| -10-----------10-⋅8-------------10 ⋅8+-t⋅10 ⋅8-----10-⋅8+-t⋅10-⋅8-

Таким образом, последний платеж равен $110 ⋅8+ t⋅ 110 ⋅8.$ Следовательно, из условия получаем:

1- -1 3- 10 ⋅8+ t⋅10 ⋅8≥ 0,92 ⇔ t ≥ 20 ⇒ r ≥ 15

Значит, наименьшая процентная ставка равна 15%.

Ответ: 15

Критерии оценки


Содержание критерия	Балл

Обоснованно получен верный ответ	2

Верно построена математическая модель	1

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	2

Ошибка.
Попробуйте повторить позже

Задача 9#1102Максимум баллов за задание: 2

На двух заводах выпускают одинаковую продукцию. Известно, что если на заводе рабочие суммарно трудятся $t2$ часов в день, то завод выпускает $t$ единиц продукции. Заработная плата на первом заводе для одного рабочего составляет $500$ рублей в час, на втором заводе – $300$ рублей в час. Определите, какое наибольшее количество товаров могут выпустить в месяц оба завода, если на зарплату в месяц рабочим выделяется $1200000$ рублей.

Источники: ЕГЭ 2017, резервный день

Показать ответ и решение

Пусть на первом заводе рабочие трудились $t2$ часов, тогда завод выпустил $t$ единиц продукции; пусть на втором трудились $p2$ часов, тогда завод выпустил $p$ продукции. Следовательно, необходимо найти наибольшее значение величины $T = t+ p$ . Так как заработная плата в час составляет $500$ и $300$ рублей на первом и втором заводах соответственно, то $1200000= 100(5t2+ 3p2)$ .
Выразим $t= T − p$ и подставим в уравнение:

2 2 2 2 1 200000 =100(5(T − p) +3p ) ⇔ 8p − 10T p+ 5T − 12000 =0

Данное уравнение должно иметь корни, следовательно, его дискриминант должен быть неотрицательным:

2 2 2 D = 100T − 4⋅8(5T − 12000) =4 ⋅8⋅12000 − 60T ≥0

Отсюда получаем, что $T2 ≤ 4⋅8⋅200= 82⋅102$ , следовательно, $T ∈ [0;80]$ (учитывая, что $T ≥ 0$ , так как это количество продукции). Следовательно, наибольшее возможное $T$ – это $T =80$ .
Проверим, получаются ли при этом целые неотрицательные значения для $t$ и $p$ (так как это количество продукции).
При $T = 80$ дискриминант $D = 0$ , следовательно,

10⋅80 p= 2⋅8 = 50 ⇒ t= 80− 50 = 30.

Таким образом, проверка удалась и ответом является $T = 80$ .

Ответ: 80

Ошибка.
Попробуйте повторить позже

Задача 10#2440Максимум баллов за задание: 2

На двух заводах производят одинаковый товар. Если на заводе рабочие суммарно трудятся $t2$ часов в неделю, то они производят $t$ товаров. Заработная плата рабочего за час работы на первом заводе составляет 500 рублей, а на втором — 200 рублей. Найдите наименьшую сумму, которую нужно потратить на зарплаты рабочим в неделю, чтобы оба завода произвели 70 единиц товара.

Источники: ЕГЭ 2017, резервный день

Показать ответ и решение

Пусть на первом заводе рабочие трудились $t2$ часов, тогда завод выпустил $t$ единиц продукции. Пусть на втором трудились $p2$ часов, тогда завод выпустил $p$ товаров. Тогда $70 = t+p.$ Так как заработная плата в час составляет 500 и 200 рублей на первом и втором заводах соответственно, то сумма, которую нужно потратить в неделю на зарплату рабочим, равна

2 2 A= 100(5t + 2p )

Выразим $t= 70− p$ и подставим в выражение для $A :$

2 A = A(p)= 100⋅7(p − 100p+ 3500)

Рассмотрим функцию

2 F(p)= p − 100 ⋅p +3500

Для того, чтобы найти наименьшее значение $A(p),$ нужно найти наименьшее значение $F(p)$ , если $p$ — целое неотрицательное число не больше 70.

Заметим, что функция $F(p)$ представляет собой квадратичную функцию, графиком которой является парабола с ветвями вверх и вершиной

100 p0 = 2 =50 ∈[0;70]

Тогда $p0$ — это точка минимума и при $p= p0$ значение функции $F (p)$ будет наименьшим.

Таким образом,

2 Amin = 700⋅F(50)= 700⋅(50 − 100⋅50+ 3500) = 700000

Ответ: 700000 рублей

Критерии оценки


Содержание критерия	Балл

Обоснованно получен верный ответ	2

Верно построена математическая модель	1

Решение не соответствует ни одному из критериев, перечисленных выше	0

Максимальный балл	2