Планиметрия на Газпроме
Ошибка.
Попробуйте повторить позже
Окружность касается продолжений двух сторон 
и 
квадрата 
со стороной 
см. Из точки 
к этой
окружности проведены две касательные. Найти радиус окружности, если угол между касательными равен 
и известно, что
Источники:
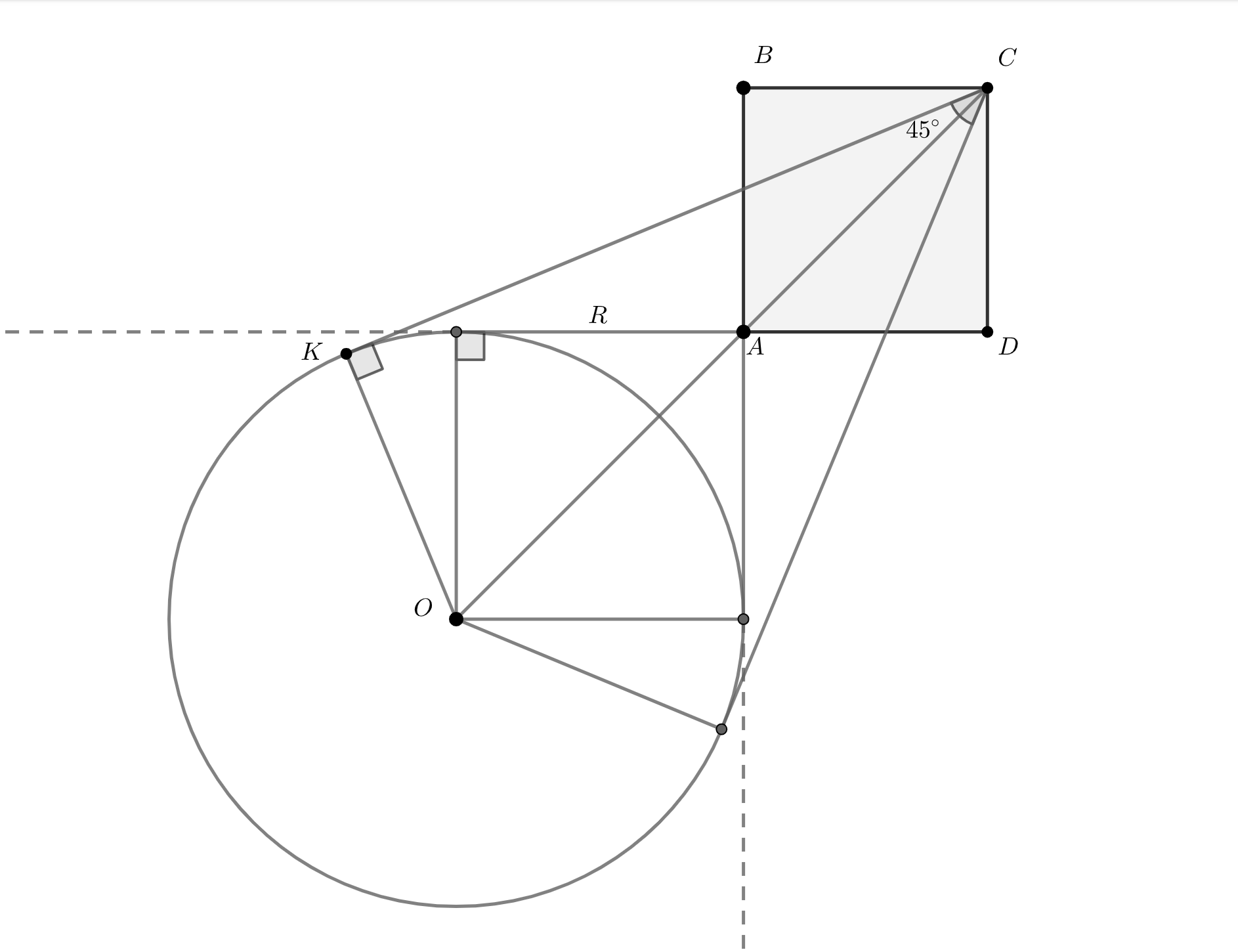
Отрезок, который отсекается от вершины 
точкой касания окружности, равен радиусу этой окружности. Диагональ 
квадрата
равна 
Если провести радиусы окружности в точки касания, то получится квадрат, со стороной 
Тогда
В результате получаем
откуда
Специальные программы
Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!
Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.
Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.
Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».
Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!
Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!
