Планиметрия на Газпроме
Ошибка.
Попробуйте повторить позже
Для охраны нефтяной платформы, расположенной в море, необходимо распределить вокруг неё 
радаров, покрытие каждого из которых
составляет круг радиуса 
км. Определить, на каком максимальном расстоянии от центра платформы их нужно
расположить, чтобы обеспечить вокруг платформы покрытие радарами кольца шириной 
км. Вычислить площадь этого кольца
покрытия.
Источники:
Чтобы обеспечить покрытие радарами кольца вокруг платформы необходимо расположить их в вершинах правильного многоугольника, центр которого совпадает с центром платформы.
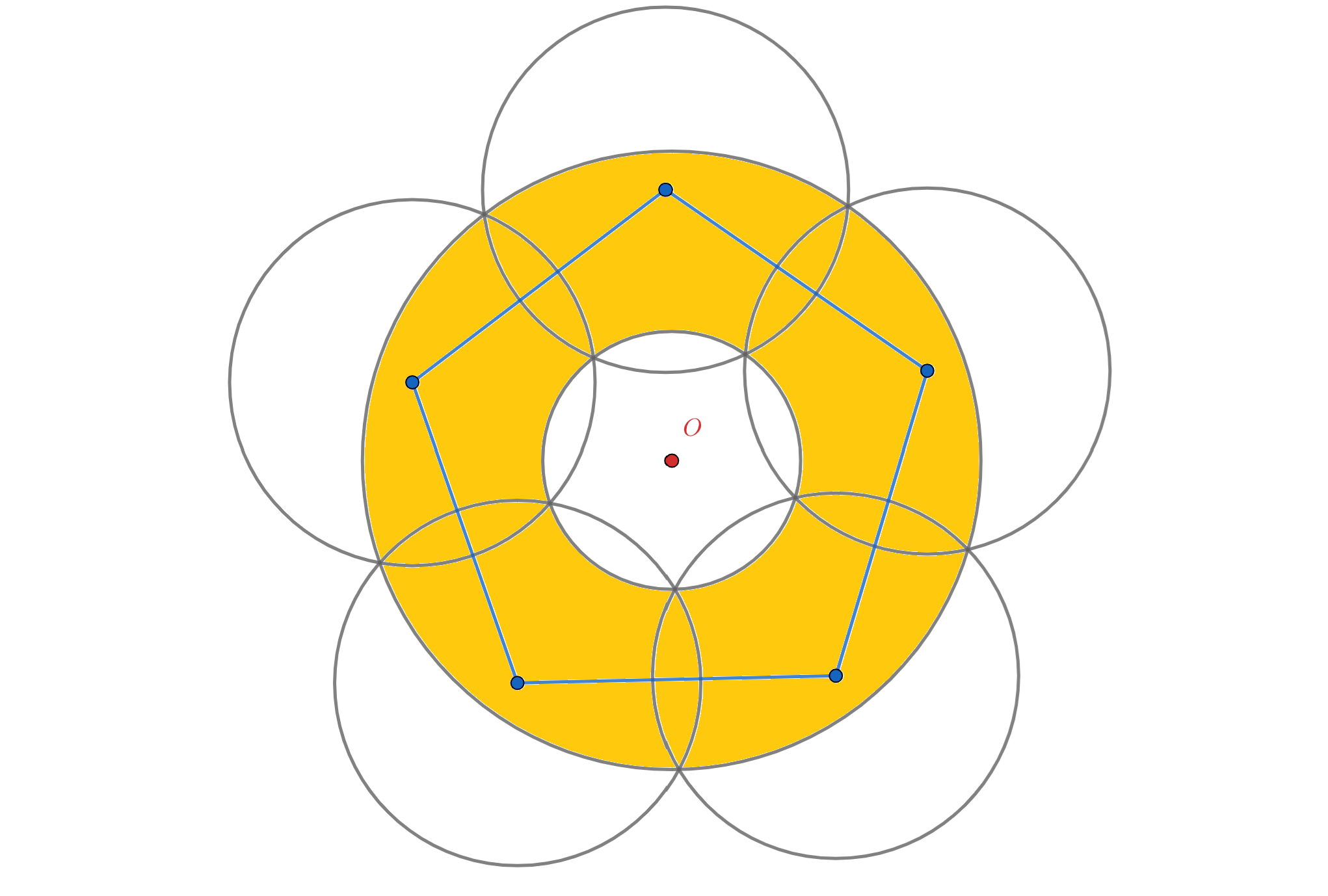
Точка 
— центр нефтяной платформы, а точки 
и 
— точки расположения радаров. Круги — это покрытие радаров. Рассмотрим
фрагмент — треугольник 
.
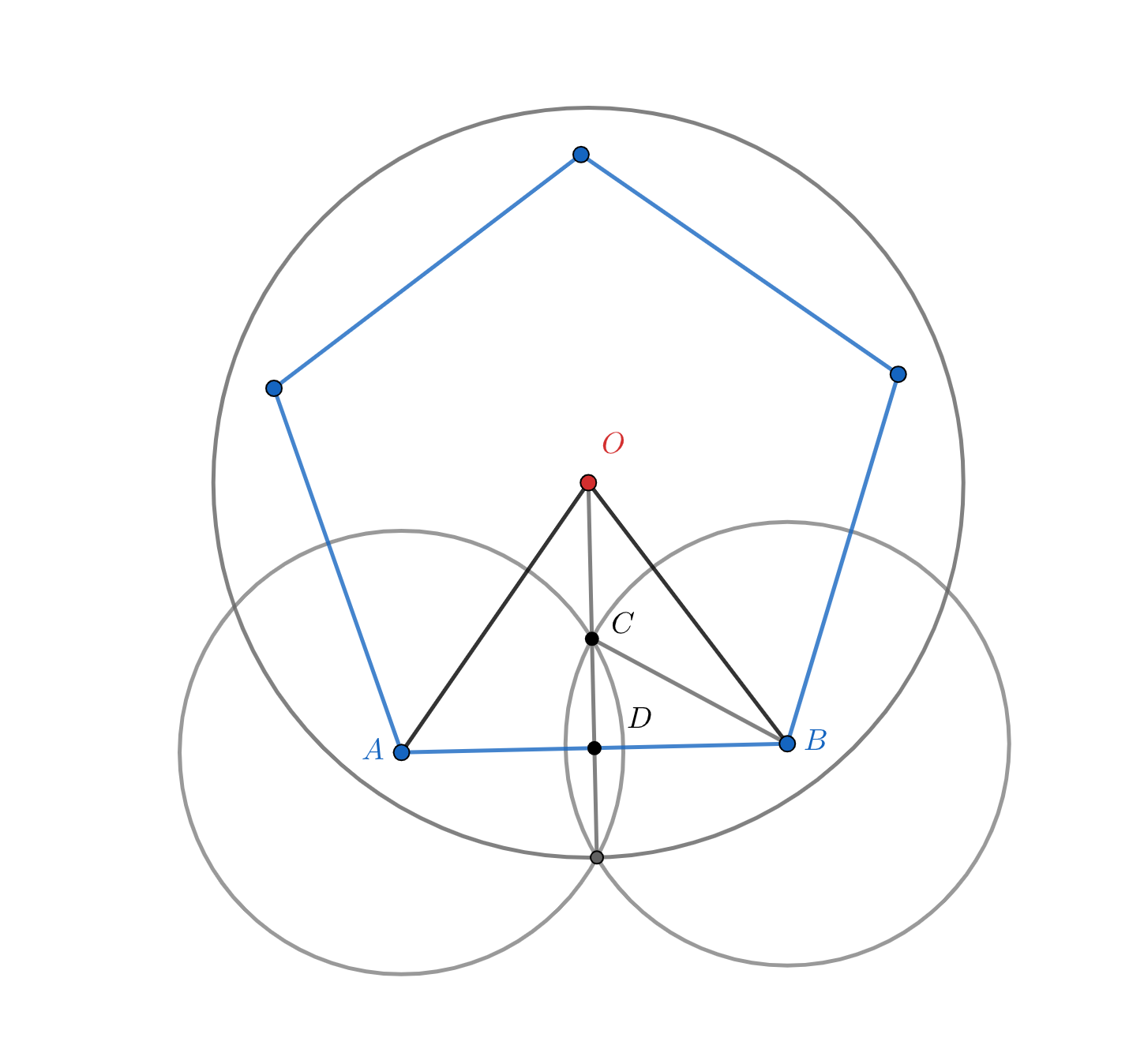
В прямоугольном треугольнике 
по теореме Пифагора найдем 
:
Тогда 
, следовательно, расстояние от центра платформы до радаров равно радиусу описанной около правильного
пятиугольника окружности:
Чтобы найти площадь кольца покрытия, нужно из площади круга с радиусом 
вычесть площадь круга с радиусом 
, то есть
. Отрезок 
равен: 
. Найдём радиусы:
откуда:
Специальные программы
Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!
Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.
Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.
Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».
Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!
Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!
