Стереометрия на Газпроме
Ошибка.
Попробуйте повторить позже
Найти радиус цилиндра с наибольшей полной поверхностью, вписанного в круговой конус высотой см и радиусом основания
см.
Источники:
Подсказка 1
Давайте вспомним, как выражается площадь полной поверхности цилиндра. Так... Нужно теперь воспользоваться условием на максимальную площадь. Как это сделать?
Подсказка 2
Конечно! Нужно выразить площадь через известные константы и радиус основания цилиндра. Для этого давайте рассмотрим осевое сечение нашей конструкции. Чем можно воспользоваться?
Подсказка 3
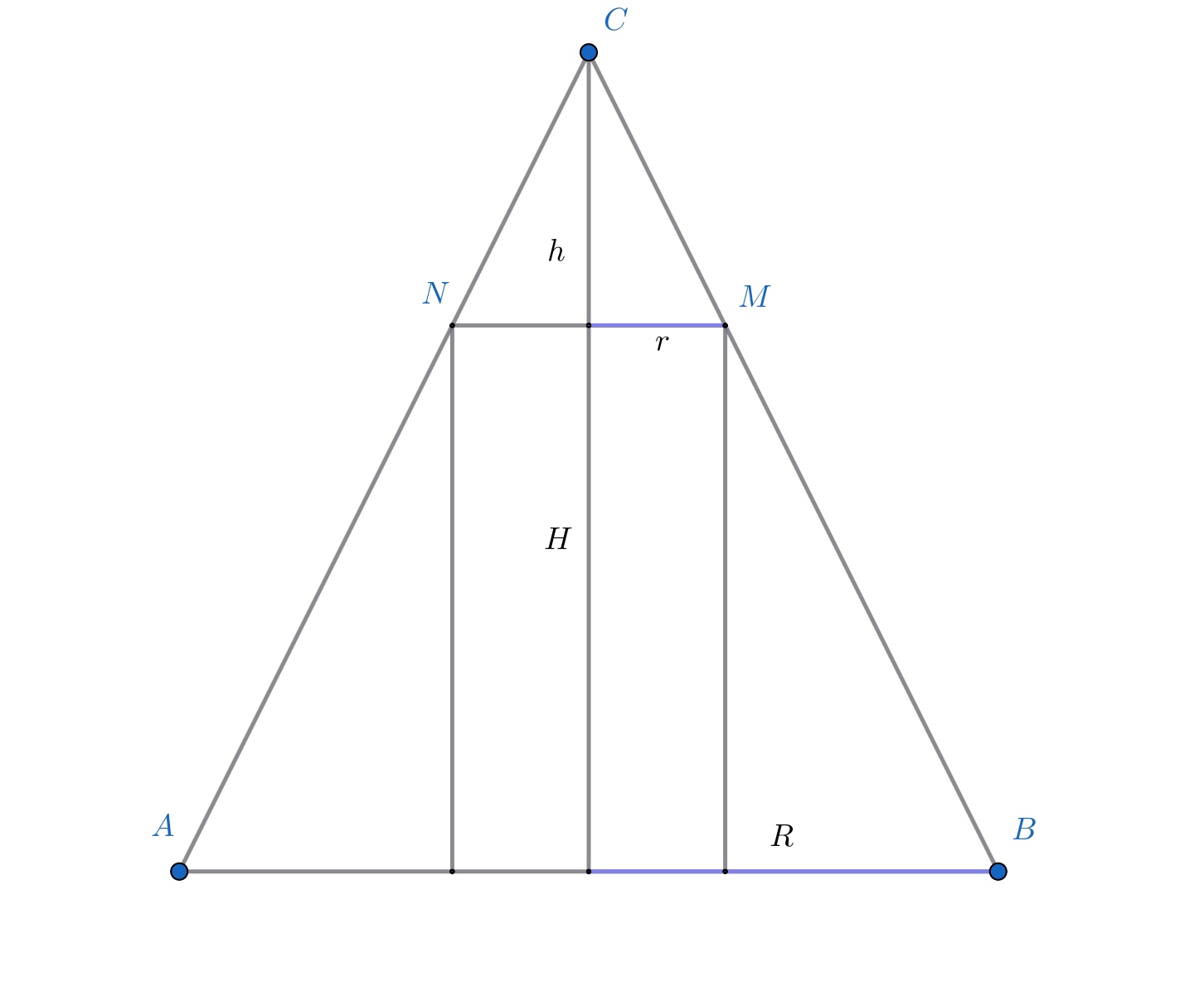
Пусть осевое сечение конуса это треугольник ABC с вершиной С, а цилиндр пересекает боковые стороны треугольника в точках M и N соответственно. Давайте распишем подобие треугольников ABC и MNC. Как, используя подобие, выразить высоту цилиндра через r и известные константы?
Подсказка 4
Да! Если H — высота конуса, h — высота цилиндра, r — радиус основания цилиндра, а R — радиус основания конуса, то из подобия получаем: R/r = H/(H-h). Отсюда легко выразить h. Подставьте это в первую формулу. Как теперь максимизировать r?
Подсказка 5
Правильно! Давайте продифференцируем S(r) и найдем максимум этой функции!
Площадь полной поверхноcти цилиндра выражается формулой
где — радиус основания цилиндра,
— высота цилиндра.
Изобразим осевое сечение цилиндра, вписанного в конус, и введём обозначения (см. рис.). Из подобия треугольников и
по
двум углам получим
отсюда
Подставим выраженное в первую формулу. Таким образом, получили функцию площади поверхности в зависимости от радиуса
основания цилиндра:
Необходимо подобрать такое значение чтобы
была максимальной. Продифференцируем это выражение:
Убедимся, что найден максимум функции проверкой знака производной:
— возрастает;
— убывает. Значит, искомое значение
равно
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!




