27.01 Стандартные кластеры
Ошибка.
Попробуйте повторить позже
Учёный решил провести кластеризацию некоторого множества звёзд по их расположению на карте звёздного неба.
Кластер звёзд – это набор звёзд (точек) на графике, лежащий внутри круга радиусом . Каждая звезда обязательно
принадлежит только одному из кластеров.
Истинный центр кластера, или центроид, – это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна.
Под расстоянием понимается расстояние Евклида между двумя точками и
на плоскости,
которое вычисляется по формуле:
В файле A хранятся данные о звёздах двух кластеров, где . В каждой строке записана информация о
расположении на карте одной звезды: сначала координата
, затем координата
. Значения даны в условных
единицах, которые представлены вещественными числами. Известно, что количество звёзд не превышает
1200.
В файле Б хранятся данные о звёздах трёх кластеров, где . Известно, что количество звёзд не превышает
15000. Структура хранения информации о звездах в файле Б аналогична файлу А.
Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: —
произведение абсцисс центров кластеров, и
– произведение ординат центров кластеров.
В ответе запишите два числа через пробел: сначала целую часть произведения для файла А, далее
целую часть произведения
для файла Б.
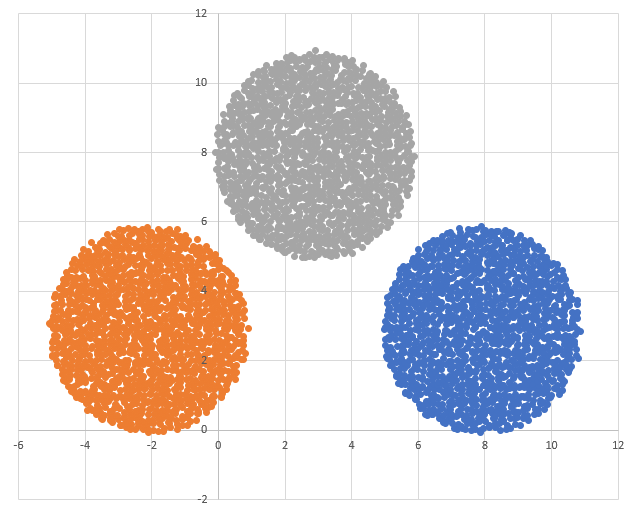
Возможные данные одного из файлов иллюстрированы графиком.
Внимание! График приведён в иллюстративных целях для произвольных значений, не имеющих отношения к заданию. Для выполнения задания используйте данные из прилагаемого файла.
Для начала визуально оценим данные в условии кластеры. Для этого откроем предложенные файлы в ,
перейдем в раздел «Вставка
Диаграммы
Точечная».
Диаграмма для файла А имеет вид:
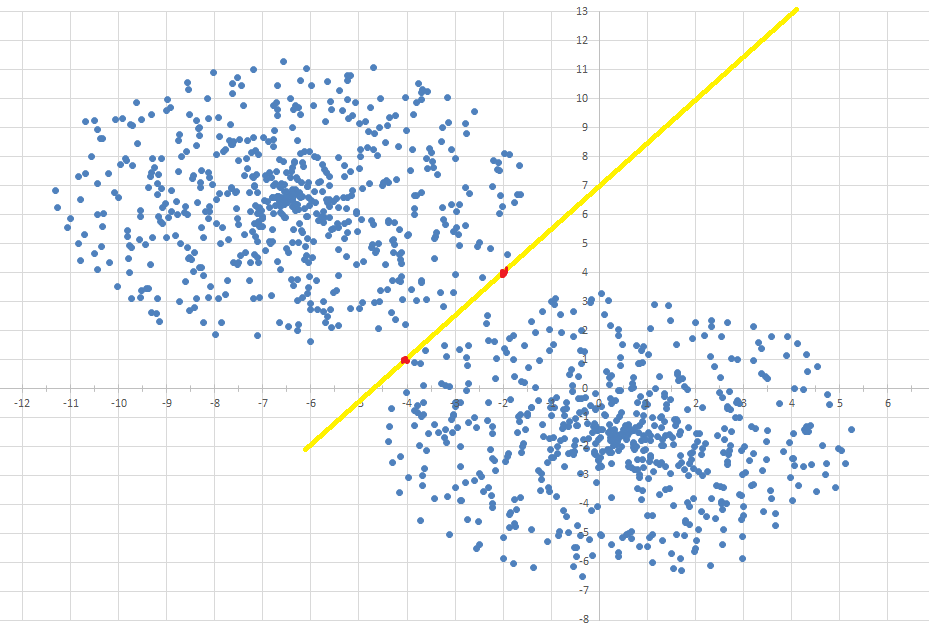
Проведем между ними прямую, разделяющую их. Прямая проходит через две точки:
Уравнение прямой по двум точкам имеет вид:
Соответственно, точки, которые удовлетворяют неравенству
принадлежат правому кластеру, а остальные – левому
Код программы для файла А:
f = open(’4A.txt’) n = f.readline() # Считываем первую строку файла с названиями столбцов a = [[] for i in range(2)] # Создаём список для кластеров for line in f: # Считваем звёзды и определяем их к кластерам x, y = list(map(float, line.replace(’,’, ’.’).split())) if y < 1.5 * x + 7: a[0].append([x, y]) else: a[1].append([x, y]) mul_x = mul_y = 1 # Переменные для произведения абсцисс и ординат центров for i in a: tx = ty = 0 # Координаты текущего центра кластера mn = 100000050000 # Минимальное расстояние for j in i: x1, y1 = j sm = 0 # Суммарное расстояние for k in i: x2, y2 = k sm += ((x2-x1)**2 + (y2-y1)**2)**0.5 if sm < mn: mn = sm tx, ty = x1, y1 mul_x *= tx mul_y *= ty print(int(mul_x * mul_y * 100))
Диаграмма для файла Б имеет вид:
Проведем между ними прямые, разделяющие их.
Первая прямая проходит через две точки:
Уравнение прямой по двум точкам имеет вид:
Соответственно, точки, которые удовлетворяют неравенству
принадлежат правому кластеру.
Вторая прямая проходит через две точки:
Уравнение прямой по двум точкам имеет вид:
Соответственно, точки, которые удовлетворяют неравенству
принадлежат левому кластеру.
Остальные точки принадлежат кластеру по центру.
Код программы для файла Б:
f = open(’4B.txt’) n = f.readline() # Считываем первую строку файла с названиями столбцов a = [[] for i in range(3)] # Создаём список для кластеров for line in f: # Считваем звёзды и определяем их к кластерам x, y = list(map(float, line.replace(’,’, ’.’).split())) if y < 1.25 * x - 2.05: a[0].append([x, y]) elif y < -0.8 * x + 1.36: a[1].append([x, y]) else: a[2].append([x, y]) mul_x = mul_y = 1 # Переменные для произведения абсцисс и ординат центров for i in a: tx = ty = 0 # Координаты текущего центра кластера mn = 100000050000 # Минимальное расстояние for j in i: x1, y1 = j sm = 0 # Суммарное расстояние for k in i: x2, y2 = k sm += ((x2-x1)**2 + (y2-y1)**2)**0.5 if sm < mn: mn = sm tx, ty = x1, y1 mul_x *= tx mul_y *= ty print(int(mul_y * mul_x * 1_000_000_000))
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!





