27.01 Стандартные кластеры
Ошибка.
Попробуйте повторить позже
Фрагмент звёздного неба спроецирован на плоскость с декартовой системой координат. Учёный решил провести
кластеризацию полученных точек, являющихся изображениями звёзд, то есть разбить их множество на
непересекающихся непустых подмножеств (кластеров), таких, что точки каждого подмножества лежат внутри
квадрата со стороной длиной
, причём эти квадраты между собой не пересекаются. Стороны квадрата не
обязательно параллельны координатным осям. Гарантируется, что такое разбиение существует и единственно для
заданных размеров квадрата.
Будем называть центром кластера точку этого кластера, сумма расстояний от которой до всех остальных точек кластера минимальна. Для каждого кластера гарантируется единственность его центра.
Расстояние между двумя точками на плоскости и
вычисляется по формуле:
В файле А хранятся координаты точек пяти кластеров, где для каждого кластера. В каждой строке
записана информация о расположении на карте одной звезды: сначала координата
, затем координата
. Известно,
что количество точек не превышает 2000.
В файле Б хранятся координаты точек трёх кластеров, где для каждого кластера. Известно, что
количество точек не превышает 10 000. Структура хранения информации в файле Б аналогична файлу
А.
Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: –
среднее арифметическое абсцисс центров кластеров и
– среднее арифметическое ординат центров
кластеров.
В ответе запишите четыре числа через пробел: сначала целую часть произведения , затем целую часть
произведения
для файла А, а затем - аналогичные данные для файла Б.
Возможные данные одного из файлов иллюстрированы графиком.
Внимание! График приведён в иллюстративных целях для произвольных значений, не имеющих отношения к заданию. Для выполнения задания используйте данные из прилагаемого файла.
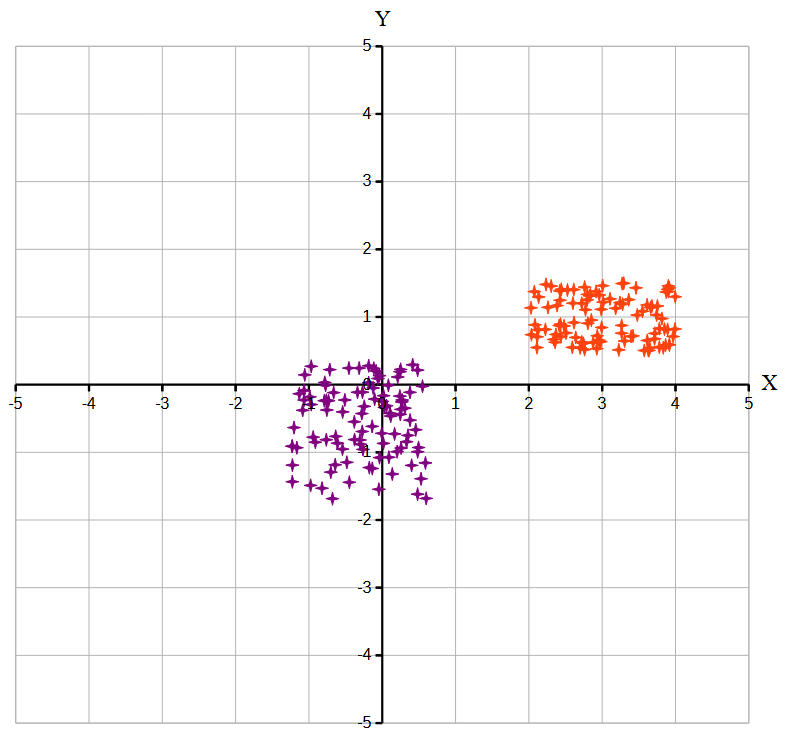
Для начала визуально оценим данные в условии кластеры. Для этого откроем предложенные файлы в ,
перейдем в раздел «Вставка
Диаграммы
Точечная».
Диаграмма для файла А имеет вид:
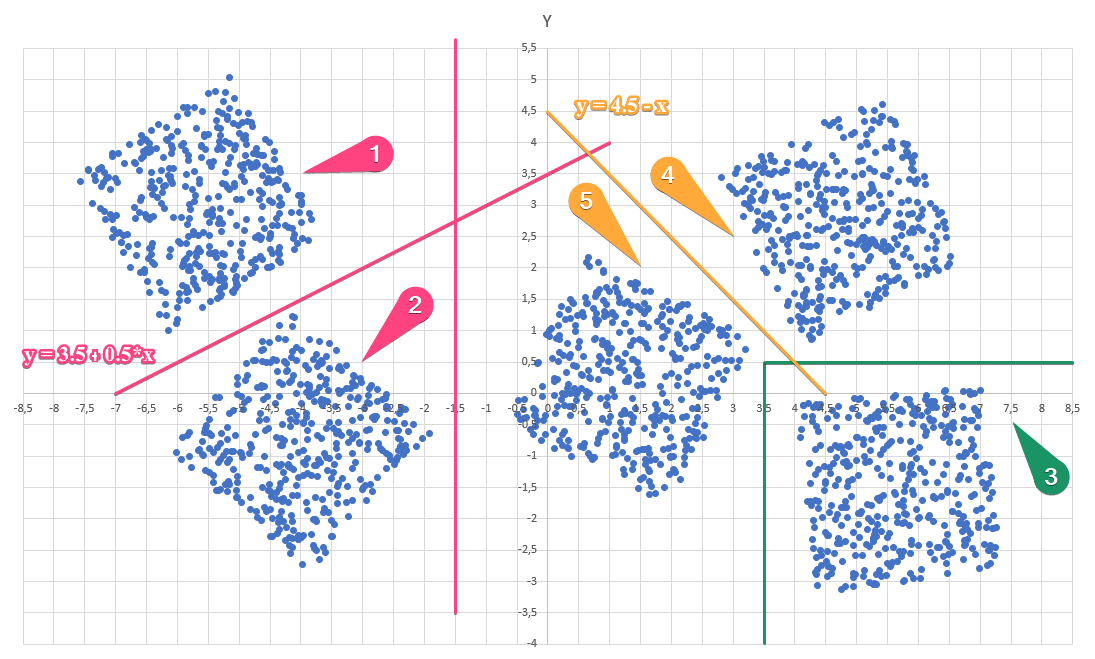
Для этих 5 кластеров необходимо провести 2 наклонных прямых, чтобы их отделить:
и
В итоге получим следующие неравенства для последовательного отделения:
1) и
2) и
3) и
4)
5) все остальные точки
Код программы для файла А:
file = open("5_A.txt")
file.readline()
clusters = [[] for i in range(5)]
for star in file:
x, y = list(map(float, star.replace(’,’, ’.’).split()))
if (y > 3.5 + 0.5*x) and (x < -1.5):
clusters[0].append((x, y))
elif (y < 3.5 + 0.5*x) and (x < -1.5):
clusters[1].append((x, y))
elif (x > 3.5) and (y < 0.5):
clusters[2].append((x, y))
elif y > 4.5 - x:
clusters[3].append((x, y))
else:
clusters[4].append((x, y))
sum_x = sum_y = 0
for cluster in clusters:
tx = ty = 0
mn = 10**20
for centroid in cluster:
x1, y1 = centroid
sm = 0
for star in cluster:
x2, y2 = star
sm += ((x2-x1)**2 + (y2-y1)**2)**0.5
if sm < mn:
mn = sm
tx, ty = x1, y1
sum_x += tx
sum_y += ty
print(int(abs(sum_x / 5) * 1000))
print(int(abs(sum_y / 5) * 1000))
Диаграмма для файла Б имеет вид:
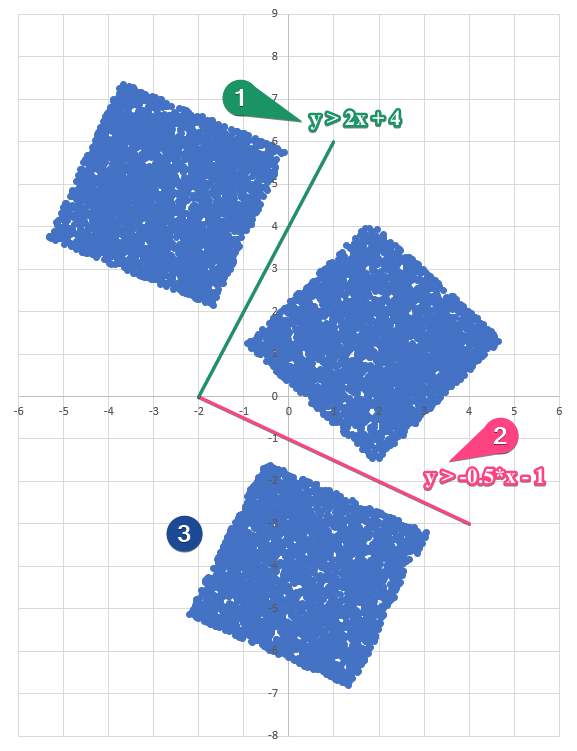
Рассмотрим 3 кластера и координаты, которыми их можно последовательно отделить:
1)
2)
3) все остальные точки
Код программы для файла Б:
file = open("5_B.txt")
file.readline()
clusters = [[] for i in range(3)]
for star in file:
x, y = list(map(float, star.replace(’,’, ’.’).split()))
if y > 2*x + 4:
clusters[0].append((x, y))
elif y > -0.5*x - 1:
clusters[1].append((x, y))
else:
clusters[2].append((x, y))
sum_x = sum_y = 0
for cluster in clusters:
tx = ty = 0
mn = 10**20
for centroid in cluster:
x1, y1 = centroid
sm = 0
for star in cluster:
x2, y2 = star
sm += ((x2-x1)**2 + (y2-y1)**2)**0.5
if sm < mn:
mn = sm
tx, ty = x1, y1
sum_x += tx
sum_y += ty
print(int(abs(sum_x / 3) * 1000))
print(int(abs(sum_y / 3) * 1000))
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!





