27.01 Поиск центроида
Ошибка.
Попробуйте повторить позже
Учёный решил провести кластеризацию некоторого множества звёзд по их расположению на карте звёздного неба.
Кластер звёзд – это набор звёзд (точек) на графике, лежащий внутри круга радиусом . Каждая звезда обязательно
принадлежит только одному из кластеров.
Истинный центр кластера, или центроид, – это одна из звёзд на графике, сумма расстояний от которой до всех остальных звёзд кластера минимальна. Центроид не вычисляется для колец, он вычисляется только для кластеров, представляющих собой круг.
Под расстоянием понимается расстояние Евклида между двумя точками и
на плоскости,
которое вычисляется по формуле:
В файле A хранятся данные о звёздах двух кластеров, где у внутреннего кластера и
у внешнего
кластера. В каждой строке записана информация о расположении на карте одной звезды: сначала координата
,
затем координата
. Значения даны в условных единицах, которые представлены вещественными числами. Известно,
что количество звёзд не превышает 1029.
В файле Б хранятся данные о звёздах четырёх кластеров, где у внутренних кластеров,
у
внешних кластеров. Известно, что количество звёзд не превышает 8166. Структура хранения информации о звездах в
файле Б аналогична файлу А.
Для каждого файла определите координаты центра каждого кластера, затем вычислите два числа: —
среднее арифметическое абсцисс центров кластеров, и
– среднее арифметическое ординат центров
кластеров.
В ответе запишите четыре числа через пробел: сначала целую часть произведения для файла А и
для файла А, далее целую часть произведения
для файла Б и
для файла
Б.
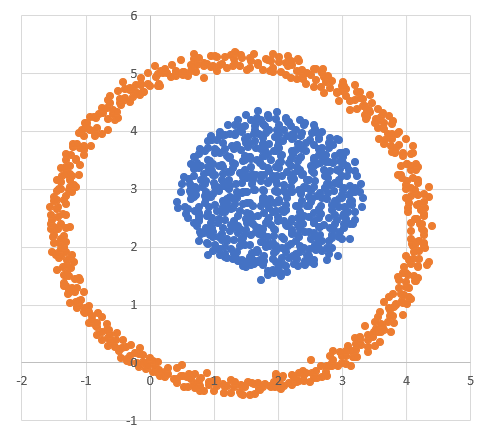
Возможные данные одного из файлов иллюстрированы графиком.
Внимание! График приведён в иллюстративных целях для произвольных значений, не имеющих отношения к заданию. Для выполнения задания используйте данные из прилагаемого файла.
Для начала визуально оценим данные в условии кластеры. Для этого откроем предложенные файлы в ,
перейдем в раздел «Вставка
Диаграммы
Точечная».
Диаграмма для файла А имеет вид:
Определим уравнение окружности, внутри которой лежит внутренний кластер. Геометрический центр внутреннего
кластера находится приблизительно в точке (0;3.5). Значит, если координаты точки удовлетворяют неравенству
окружности: , тогда эта звезда относится ко внутреннему кластеру.
Код программы для файла А:
f = open(’27_5_A.txt’) n = f.readline() cluster = [] for i in range(1029): star = list(map(float, f.readline().replace(’,’, ’.’).split())) x, y = star[0], star[1] if x ** 2 + (y - 3.5) ** 2 <= 2.1 ** 2: cluster.append(star) sum_x = sum_y = tx = ty = 0 mn = 100000050000 for j in cluster: x1, y1 = j sm = 0 for k in cluster: x2, y2 = k sm += ((x2 - x1) ** 2 + (y2 - y1) ** 2) ** 0.5 if sm < mn: mn = sm tx, ty = x1, y1 sum_x += tx sum_y += ty print(int(sum_x * 525)) print(int(sum_y * 525))
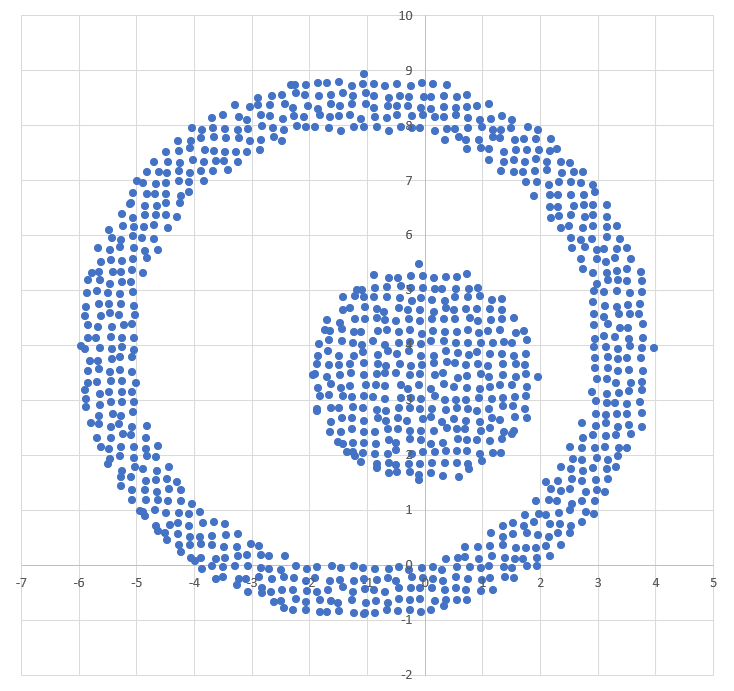
Диаграмма для файла Б имеет вид:

Нанесём на график прямую: :

Теперь можем провести определить какие звезды к каким кластерам относятся.
Сначала разделим на группы по два кластера.
Точки, которые удовлетворяют неравенству: находятся в верхней (первой) группе.
Точки, которые удовлетворяют неравенству: находятся в нижней (второй) группе.
Рассмотрим подробно первую группу:
Радиус внутренний кластер равен , геометрический центр кластера находится в точке (8;7). Следовательно, если
координаты точки удовлетворяют неравенству окружности:
, тогда эта звезда относится ко
внутреннему кластеру первой группы.
Рассмотрим подробно вторую группу:
Радиус внутренний кластер равен , геометрический центр кластера находится в точке (2;2). Следовательно, если
координаты точки удовлетворяют неравенству окружности:
, тогда эта звезда относится ко
внутреннему кластеру второй группы.
Код программы для файла Б:
f = open(’27_3_B.txt’) n = f.readline() clusters = [[] for i in range(2)] for i in range(8166): star = list(map(float, f.readline().replace(’,’, ’.’).split())) x, y = star[0], star[1] if y >= 9.5 - x: if (x - 8) ** 2 + (y - 7) ** 2 < 2.1 ** 2: clusters[0].append(star) else: if (x - 2) ** 2 + (y - 2) ** 2 < 2.1 ** 2: clusters[1].append(star) sum_x = sum_y = 0 for i in clusters: tx = ty = 0 mn = 100000050000 for j in i: x1, y1 = j sm = 0 for k in i: x2, y2 = k sm += ((x2 - x1) ** 2 + (y2 - y1) ** 2) ** 0.5 if sm < mn: mn = sm tx, ty = x1, y1 sum_x += tx sum_y += ty print(int(sum_x / len(clusters) * 300)) print(int(sum_y / len(clusters) * 300))
Специальные программы

Программа
лояльности v2.0
Приглашай друзей в Школково и получай вознаграждение до 10%!

Крути рулетку
и выигрывай призы!
Крути рулетку и покупай курсы со скидкой, которая привязывается к вашему аккаунту.

Бесплатное онлайн-обучение
Для школьников из приграничных территорий России, проживающих в ДНР, ЛНР, Херсонской, Запорожской, Белгородской, Курской, Брянской областях и Крыму.

Налоговые вычеты
Узнай, как получить налоговый вычет при оплате обучения в «Школково».

Специальное предложение
для учителей
Бесплатный доступ к любому курсу подготовки к ЕГЭ, ОГЭ и олимпиадам от «Школково». Мы с вами делаем общее и важное дело, а потому для нас очень значимо быть чем-то полезными для учителей по всей России!

Вернём деньги за курс
за твою сотку на ЕГЭ
Сдать экзамен на сотку и получить обратно деньги за подготовку теперь вполне реально!





