Тема ММО - задания по годам

ММО 2024

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела ммо - задания по годам

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#85482

В остроугольном треугольнике $ABC$ высоты $AH ,BH A B$ и $CH C$ пересекаются в точке $H$ . Через точки, в которых окружность радиуса $HHA$ с центром $H$ пересекает отрезки $BH$ и $CH$ , проведена прямая $ℓA$ . Аналогично проведены прямые $ℓB$ и $ℓC$ . Докажите, что точка пересечения высот треугольника, образованного прямыми $ℓA,ℓB,ℓC$ , совпадает с центром окружности, вписанной в треугольник $ABC$ .

Источники: ММО - 2024, второй день, 11.4 (см. mmo.mccme.ru)

Подсказки к задаче

Подсказка 1

Нарисуйте большой и правильный чертёж к задаче! Линейкой и циркулем. Желательно 2 раза, в разных конфигурациях.

Подсказка 2

Если вы это сделали, то увидите, что прямые l_B и l_C подозрительным образом пересекаются на биссектрисе угла A. Аналогично для других пар. Попробуем это доказать?)

Подсказка 3

Пусть l_B и l_C пересекают отрезки СH и BH в точках Q и P соответственно. l_B и l_C пересекаются в точке X. ∠BAC = 2a, ∠CBA = 2b, ∠ACB = 2c. Несложным счётом углов докажите, что ∠H_CHP = ∠N_BHQ = 2a. Какой вывод тогда можно сделать?

Подсказка 4

Так как H_CH = HP (по условию), то ∠H_CPH = 90 - a, аналогично ∠H_BQH = 90 - a. Значит, PH_CH_BQ — вписанный. Теперь пусть l_B, l_C пересекают AH в точках V и U соответственно. Что теперь можно сказать про треугольники PUH и QHV?

Подсказка 5

Верно! Они равнобедренные. Несложным счётом углов докажите, что ∠XPH = c, ∠XPH_C = b, а также, что ∠H_CQX = b. Не забывайте, что a+b+c=90. Что мы тогда получаем?

Подсказка 6

Именно! Мы получаем, что X лежит на окружности H_CPQ, то есть на окружности PH_CH_BQ. Вновь посчитав углы, докажите, что H_CX и H_BX — биссектрисы углов ∠AH_CH_B и AH_BH_C. Что из этого следует?

Подсказка 7

То, что AX — биссектриса угла H_CAH_B, то есть AX — биссектриса ∠BAC. Мы доказали, что l_B и l_C пересекаются на биссектрисе ∠BAC. Аналогично докажем это для других пар. Осталось доказать, что XI ⊥ RS, где R, S - точки пересечения l_A с отрезками BH и CH соответственно. Но X лежит на AI, где I — центр вписанной окружности треугольника ABC. Значит нужно доказать, что AI ⊥ RS, потом аналогично докажем это для других пар и задача убита. Итак, приступим. Какой вывод можно сделать про RS в треугольнике RHS? Не забывайте, мы сейчас думаем о биссектрисах.

Подсказка 8

Действительно, RS ⊥ биссектрисе ∠RHS, пусть это прямая p_A. Тогда перпендикулярность AI и RS равносильна параллельности p_A и AI. Оставим это несложное утверждение вам) Успехов!

Показать доказательство

Покажем, что биссектрисы треугольника $ABC$ содержат высоты треугольника, образованного прямыми $ℓ ,ℓ ,ℓ A B C$ . Для этого докажем, что точка пересечения прямых $ℓB,ℓC$ лежит на биссектрисе угла $∠BAC$ , а прямая $ℓA$ перпендикулярна этой биссектрисе.

_________________________________________________________________________________________________________________________________________________________________________________

Докажем, что прямая $ℓA$ перпендикулярна биссектрисе угла $∠BAC$ .

Пусть $R$ и $S$ - это точки пересечения окружности с центром в $H$ радиуса $HHA$ с отрезками $BH$ и $CH$ соответственно. Тогда треугольник $RHS$ - равнобедренный с основанием $RS$ , поэтому прямая $RS$ (она же $ℓA$ ) перпендикулярна прямой $pA$ , содержащей биссектрису угла $∠BHC$ . Поэтому достаточно доказать, что прямая $pA$ параллельна биссектрисе угла $∠BAC$ .

$PIC$

Пусть $MA$ и $NA$ — середины дуг $HCHHB$ и $⌣ HBAHC$ окружности $ωA$ , построенной на $AH$ как на диаметре. Из свойств вписанных углов следует, что $AMA$ — биссектриса $∠BAC,HNA$ — биссектриса $∠HCHHB$ . Заметим также, что $MANA$ - диаметр окружности $ωA$ . Значит, отрезки $MANA$ и $AH$ пересекаются в центре окружности $ωA$ как её диаметры и делятся точкой пересечения пополам. То есть четырёхугольник $AMAHNA −$ параллелограмм (и даже прямоугольник, поскольку его углы - вписанные, опирающиеся на диаметры окружности $ωA$ , то есть прямые). В частности, $AMA ∥HNA$ , что и требовалось.

_________________________________________________________________________________________________________________________________________________________________________________

Докажем, что прямые $ℓ B$ и $ℓ C$ пересекаются на биссектрисе угла $∠BAC$ .

Пусть прямые $ℓ B$ и $ℓ C$ пересекают отрезки $BH, CH$ в точках $P$ и $Q$ соответственно, а точку пересечения $ℓ B$ и $ℓ C$ обозначим через $X$ . Также обозначим углы $∠A,∠B$ и $∠C$ треугольника $ABC$ через $2α,2β$ и $2γ$ соответственно.

$PIC$

Поскольку $HP = HHC$ и $HQ = HHB$ , то треугольники $HHCP$ и $HHBQ$ - равнобедренные с углами, равными $∠HCHB = ∠BAC = 2α$ , напротив оснований. Поэтому $∠HP HC = ∠HQHB =90∘− α= β+ γ$ . Пусть прямые $ℓB$ и $ℓC$ пересекают отрезок $AH$ в точках $U$ и $V$ соответственно. Тогда треугольник $PUH$ - равнобедренный с основанием $PU$ , значит $∠XP H = ∠UPH = 180∘−∠2BHA-= γ$ . Рассуждая аналогично для треугольника $QV H$ , получаем, что $∠XQH = β$ . Тогда получаем

∠XP HC =∠HP HC − ∠HP X = β+ γ− γ = β =∠XQHC,

откуда следует, что $X$ лежит на окружности, описанной около треугольника $HCP Q$ . Аналогично точка $X$ лежит на окружности, описанной около треугольника $HBP Q$ . Таким образом, пять точек $X,HB$ , $P,Q,HC$ лежат на одной окружности.

Тогда по свойству вписанных углов $∠XHBHC = ∠XQHC =β$ . Четырёхугольник $BHCHBC −$ вписанный, поскольку $∠BHCC = ∠BHBC = 90∘$ . Значит, $∠HCHBC = 180∘− ∠ABC =180∘− 2β$ , то есть $∠AHBHC = 2β$ . Отсюда следует, что $HBX$ - биссектриса угла $∠AHBHC$ . Аналогично $HCX −$ биссектриса угла $∠AHCHB$ . Значит, точка $X$ является центром окружности, вписанной в треугольник $AHBHC$ , в частности, лежит на биссектрисе угла $∠BAC$ .

_________________________________________________________________________________________________________________________________________________________________________________

Повторяя рассуждения для двух других биссектрис треугольника $ABC$ , получаем, что точка пересечения биссектрис треугольника $ABC$ совпадает с точкой пересечения высот треугольника, образованного прямыми $ℓ ,ℓ ,ℓ . A B C$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#85483

Петя и Вася независимо друг от друга разбивают белую клетчатую доску $100 ×100$ на произвольные группы клеток, каждая из чётного (но не обязательно все из одинакового) числа клеток, каждый - на свой набор групп. Верно ли, что после этого всегда можно покрасить по половине клеток в каждой группе из разбиения Пети в чёрный цвет так, чтобы в каждой группе из разбиения Васи было поровну чёрных и белых клеток?

Источники: ММО - 2024, второй день, 11.5 (см. mmo.mccme.ru)

Подсказки к задаче

Подсказка 1

Понятно, что вариантов таких разбиений очень и очень много, разбирать каждый из них просто неразумно. Подумайте, какое существует частное разбиение, которое при этом описывает любое другое. Обратите внимание, что по условию разбиения состоят из групп четного числа клеток.

Подсказка 2

Существует частное разбиение, когда все группы и у Пети, и у Васи содержат в точности по две клетки. С другой стороны, любое разбиение на группы из четного числа клеток можно измельчить на группы из двух клеток, и если существует требуемая раскраска для измельченных разбиений, то та же самая раскраска, очевидно, решает задачу и для исходных разбиений. Подумайте, на какие два вида можно поделить полученные после «измельчения» пары клеток.

Подсказка 3

Будут группы, которые совпадают полностью, и те, что совпадают только одной клеткой из двух. Первые очень легко раскрасить нужным нам образом. А вот что делать с группами второго типа? Вообще, когда мы говорим о раскраске каких-то групп, связанных между собой, какая идея представления этих групп и связей между ними в первую очередь всплывает в сознании?

Подсказка 4

Давайте представим наши группы по две клетки в виде вершин графа, при этом две вершины графа соединены ребром тогда и только тогда, когда имеют общую клетку и разного «хозяина». Что за граф мы таким образом получим?

Подсказка 5

Каждая группа имеет две клетки, значит, степень каждой вершины графа равна двум, при этом каждое ребро соединяет Васину и Петину группы, значит, наш граф является двудольным. Осталось только вспомнить особенность циклов в таком графе и покрасить его ребра в два цвета.

Показать ответ и решение

Первое решение.

Заметим, что частным случаем разбиений является ситуация, когда каждая из Петиных и Васиных групп содержит в точности две клетки. С другой стороны, любое разбиение на группы из четного числа клеток можно измельчить на группы из двух клеток, и если существует требуемая раскраска для измельченных разбиений, то та же самая раскраска, очевидно, решает задачу и для исходных разбиений.

Теперь каждую Васину группу (из двух клеток), совпадающую с какой-то из Петиных групп, покрасим в черный и белый цвет любым из двух способов - одну клетку в черный, другую в белый цвет.

Осталось раскрасить множество клеток, которое Васей и Петей разбито на пары так что ни одна Васина пара не совпадает с Петиной парой.

Построим граф, вершины которого соответствуют Васиным и Петиным группам (у Васи и Пети, очевидно, одно и то же количество групп). Две вершины соединим ребром тогда и только тогда, когда соответствующие группы имеют общую клетку. Тогда каждая вершина графа имеет степень два, причем любое ребро соединяет одну из вершин, соответствующих Васиным группам, с одной из вершин, соответствующих Петиным группам.

Такой граф разбивается на циклы, причем каждый цикл имеет четную длину (за счет того, что в нем чередуются вершины, соответствующие Васиным и Петиным групам) и допускает раскраску в два цвета, при которой цвета ребер чередуются вдоль цикла. Наконец, цвету клетки сопоставим цвет ребра, соединяющего две вершины графы, соответствующие Васиной и Петиной группам, пересекающимся по данной клетке. Полученная раскраска удовлетворяет условию задачи.

_________________________________________________________________________________________________________________________________________________________________________________

Второе решение.

Для удобства назовём непересекающиеся группы клеток одного разбиения (Пети или Васи) фигурками.

Построим вспомогательный двудольный граф G. Для каждой из фигурок одного из разбиений (Пети или Васи) добавим в граф $G$ новую, соответствующую этой фигурке вершину. При этом вершины, соответствующие фигуркам Пети, отнесём к первой доле, а вершины, соответствующие фигуркам Васи, - ко второй. Далее проведём рёбра между некоторыми вершинами графа $G$ по следующему правилу: если фигурка Пети $A$ пересекается с фигуркой Васи $B$ по нечётному количеству клеток, то проведём между соответствующими этим фигуркам вершинами ребро.

Заметим, что в построенном графе степень каждой вершины чётна. Действительно, выберем, например, произвольную фигурку Васи $A$ . Поскольку $A$ состоит из чётного числа клеток и пересекается лишь с фигурками из разбиения Пети, то по нечётному количеству клеток она будет пересекаться с чётным количеством фигурок.

Рассмотрим произвольную компоненту связности $G$ . Поскольку степень каждой вершины этой компоненты чётна, то существует цикл (т.н. эйлеров цикл), проходящий по всем рёбрам этой компоненты ровно по 1 разу. Выберем такие циклы для каждой компоненты связности $G$ . Для удобства назовём полученное разбиение рёбер графа $G$ на циклы $Ω$ .

Теперь построим искомую раскраску фигурок в разбиении Пети. Выберем произвольный цикл $σ$ из построенного разбиения $Ω$ и ориентируем его рёбра в каком-то из двух возможных естественных направлений его обхода. Рассмотрим произвольное (уже ориентированное) ребро $\text{[math]}$ цикла $σ$ . Пусть оно соединяет вершины, соответствующие фигуркам $A$ и $B$ . По построению фигурки $A$ и $B$ пересекаются по нечётному количеству клеток. Пусть они пересекаются по $2k+ 1$ клетке. Тогда если ребро $e$ ведёт из первой доли во вторую, то Петя покрасит произвольные $k$ из них в чёрный цвет и произвольные $k+1$ из них в противном случае. Пусть Петя выполнит аналогичную покраску для каждой компоненты связности $G$ . Наконец, пусть для каждой пары фигурок $A$ и $B$ , пересекающихся по чётному количеству клеток, Петя покрасит ровно половину клеток в их пересечении в чёрный цвет.

Докажем, что полученная покраска будет искомой. Рассмотрим, например, произвольную фигурку Пети $A$ . Пусть $B$ - произвольная фигурка Васи. Заметим, что среди общих клеток фигурок $A$ и $B$ разность числа чёрных и белых клеток равна $± 1$ или 0 , в зависимости от чётности числа клеток в этом пересечении. Поэтому достаточно доказать, что разность +1 встречается среди пересечений фигурки Пети $A$ с фигурками Васи столько же раз, сколько и разность -1 . Пусть фигурке $A$ в графе $G$ соответствует вершина $v$ , которая лежит в некотором цикле $σ$ из построенного ранее разбиения $Ω$ . Тогда каждой разности +1 соответствует ребро цикла $σ$ , входящее в $v$ , а каждой разности -1 - ребро цикла $σ$ , исходящее из $v$ . Из построения цикла $σ$ следует, что рёбер, входящих в $v$ , в нём будет столько же, сколько и рёбер, исходящих из $v$ . Поэтому фигурок Васи, в клетках пересечения $A$ с которыми будет ровно на одну чёрную клетку больше, будет столько же, сколько фигурок Васи, в клетках пересечения $A$ с которыми будет ровно на одну белую клетку больше. Таким образом, в фигурке $A$ поровну чёрных и белых клеток.

Ответ: да

Ошибка.
Попробуйте повторить позже

Задача 3#85484

Докажите, что если при $n∈ ℕ$ число $2+ 2√12n2+-1$ целое, то оно точный квадрат.

Источники: ММО - 2024, второй день, 11.3 (см. mmo.mccme.ru)

Подсказки к задаче

Подсказка 1

Внимательно посмотрим на выражение. Если наше выражение целое при любых натуральных n, то оно четное. Обозначим его за 2k.

Подсказка 2

Что можно сказать про k после возведения в квадрат полученного уравнения на n и k?

Подсказка 3

Что k — чётное, то есть k = 2m. Получили, что произведение взаимно простых равно квадрату числа. А часто ли такое происходит?

Подсказка 4

Нужно разобрать 2 случая, один из которых не подойдет из-за остатков по модулю 3

Показать доказательство

Если число $2+ 2√12n2+1-$ целое при $n∈ ℕ$ , то оно чётное. Обозначим $2 +2√12n2+-1=$ $2k,k ∈ℕ$ . Тогда $√12n2+-1= k− 1$ . Возводя это равенство в квадрат, получаем

2 2 12n = k − 2k

Число $k$ чётное: $k= 2m$ , где $m ∈ ℕ$ .

Тогда

2 2 12n = 4m − 4m

3n2 =(m − 1)m

Поскольку числа $m$ и $m − 1$ взаимно просты, следует рассмотреть два случая:

1) $m− 1= u2,m = 3v2$ , где $u,v ∈ ℕ,u⋅v = n$ ;

2) $m− 1= 3u2,m = v2$ , где $u,v ∈ ℕ,u⋅v = n$ .

В первом случае имеем $3v2− 1= u2$ , то есть $u2$ даёт остаток 2 при делении на 3 . Это невозможно, так как точный квадрат может давать при делении на 3 только остатки 0 или 1.

Во втором случае получаем $2+ 2√12n2+-1= 4m =(2v)2$ - точный квадрат.

Ошибка.
Попробуйте повторить позже

Задача 4#85486

Чемпионат по футболу проходил в два круга. В каждом круге каждая команда сыграла с каждой один матч (за победу даётся три очка, за ничью одно, за поражение ноль). Оказалось, что все команды вместе набрали в первом круге $60%$ от общей суммы всех очков за два круга. Известно также, что победитель чемпионата набрал во втором круге в 30 раз меньше очков, чем все команды вместе в первом круге. Сколько команд участвовало в турнире?

Источники: ММО - 2024, второй день, 11.2 (см. mmo.mccme.ru)

Подсказки к задаче

Подсказка 1

Если в первом туре они набрали 60% от общей суммы очков, то выходит во втором туре они набрали 40% от общего числа очков. То есть в первом круге они набрали в 1,5 раза больше чем во втором. Как-будто это очень немало. Отсюда, хотелось бы сделать оценку на количество очков набранных за один тур.

Подсказка 2

Давайте посмотрим на один матч. За каждый матч суммарно команды получили либо 2, либо 3 очка. Но в таком случае, так как количество игр равно n(n-1)/2, где n - количество команд, то как мы можем оценить суммарное кол-во очков?

Подсказка 3

Верно, мы можем оценить, что количество очков за один тур расположено от 2*n(n-1)/2 до 3*n(n-1)/2. Значит, если количество очков в двух турах отличается в 1,5 раза, то так как во втором туре хотя бы 2*n(n-1)/2, а в первом не более 3*n(n-1)/2, то их отношение хотя бы 3/2. При этом, понятно, что тогда в первом туре ровно 3n(n-1)/2 очков, а во втором ровно 2n(n-1)/2. Но тогда, в первом туре ничьей не было, а во втором все сыграли в ничью. Осталось только применить это знание и факт того, что победитель во втором туре набрал в 30 раз меньше очков чем все суммарно в первом и получить ответ.

Показать ответ и решение

Пусть в турнире участвовало $n$ команд. Заметим, что в каждом матче две команды в сумме получают 2 или 3 очка. Значит, общее количество очков, которые могут набрать все команды в одном круге, не меньше, чем $n(n−1) 2⋅ 2$ , и не больше, чем $n(n−1) 3⋅ 2$ . Из условия следует, что все команды вместе набрали в первом круге ровно в полтора раза больше очков, чем во втором ( $60%$ всех очков в первом круге и $40%$ во втором). Но это возможно лишь в случае, если в первом круге все матчи закончились победой одной из команд (общая сумма очков $n(n−1) 3 ⋅ 2$ ), а во втором - ничьей (общая сумма очков $n(n−1) 2⋅ 2$ ). Значит, победитель набрал во втором круге $n− 1$ очков. По условию, $n(n−1) 30⋅(n− 1)=3⋅ 2$ , откуда находим $n =20$ .

Ответ: 20

Ошибка.
Попробуйте повторить позже

Задача 5#85487

Существует ли на координатной плоскости точка, относительно которой симметричен график функции $f(x)= -1-- 2x+1$ ?

Источники: ММО - 2024, второй день, 11.1 (см. mmo.mccme.ru)

Подсказки к задаче

Подсказка

Давайте подумаем, что нам даст факт того, что относительно какой-то точки график симметричен? Это значит, что если - это точка а, то f(x) - a - нечетная. Давайте тогда, попробуем найти такие а, что f(x) - a + f(-x) - a = 0(условие на нечетность). После того как мы это запишем, то получим то некоторое условие на а.

Показать ответ и решение

Покажем, что функция $g(x)= f(x)− 1 2$ является нечётной. Действительно,

---1-- 1 -2x-- 1 1 -1--- g(− x) =2−x +1 − 2 = 2x+ 1 − 2 = 2 − 2x +1 =− g(x).

Следовательно, график функции $g$ симметричен относительно начала координат, а график функции $f$ симметричен относительно точки $( ) 0,12$ .

Ответ: да

Ошибка.
Попробуйте повторить позже

Задача 6#85488

Кощей придумал для Ивана-дурака испытание. Он дал Ивану волшебную дудочку, на которой можно играть только две ноты — до и си. Для прохождения испытания Ивану нужно сыграть какую-нибудь мелодию из 300 нот на свой выбор. Но до того, как он начнёт играть, Кощей выбирает и объявляет запретными одну мелодию из пяти нот, одну — из шести нот, $...$ , одну — из 30 нот. Если в какой-то момент последние сыгранные ноты образуют одну из запретных мелодий, дудочка перестаёт звучать. Сможет ли Иван пройти испытание, какие бы мелодии Кощей ни объявил запретными?

Источники: ММО - 2024, первый день, 11.6 (см. mmo.mccme.ru)

Подсказки к задаче

Подсказка 1

Запретные отрывки нам неизвестны, их очень много, поэтому рассматривать то, как они пересекаются, может быть невозможно. Однако было бы очень удобно из большого количества длинных мелодий вычеркивать те, которые запрещаются каждым из запретных отрывков. Попробуем придумать такие длинные мелодии.

Подсказка 2

Понятно, что хаотично придумывать мелодии не только сложно, но и бессмысленно (мы не сможем уследить, какие отрывки их запрещают). Значит, нам нужно как-то красиво и последовательно их строить, чтобы знать, как они выглядят. Также подумаем, а сколько мелодий может запрещать конкретный отрывок длины k?

Подсказка 3

А давайте попробуем строить периодические бесконечные мелодии! Но периода какой длины нам хватит?

Подсказка 4

Обратите внимание на то, что при подсчёте количества мелодий, которые запрещает конкретный отрывок длины k, мы будем вычеркивать не более 2^(l-k) мелодий, где l — длина периода.

Показать ответ и решение

Первое решение.

Рассмотрим всевозможные мелодии из нот до и си длины $13$ , коих $13 2$ штук. Каждую такую мелодию периодически продолжим в обе стороны, получив бесконечную в обе сторону мелодию. Назовём две получившиеся бесконечные мелодии эквивалентными, если одна получается из другой сдвигом.

Наименьший период всех бесконечных мелодий, кроме двух, состоящих только из нот до и только из нот си, равен $13.$ Количество не эквивалентных друг другу бесконечных мелодий равно

213− 2 --13--+ 2= 632

(каждой бесконечной мелодии $X$ периода $13$ эквиваленты $13$ мелодий (включая саму $X$ с периодом, который будет циклическим сдвигом $13$ нот, дающих мелодию $X$ )

Из них мелодий, содержащих запрещённые Кощеем мелодии, не больше

(28+ 27 +...+ 21)+18= 528

(в скобках учтены запретные мелодии длины $≤ 12$ , полученные дописыванием $k$ символов к запретной мелодии длины $13− k$ , а за скобками — все остальные).

Таким образом, найдётся бесконечная мелодия, которая не содержит запретных мелодий, и для прохождения испытания Ивану достаточно сыграть её кусок длины $300.$

______________________________________________________________________________________________________________________________________________________

Второе решение.

Пусть $Ln$ - число мелодий длины $n$ , не содержащих запретных последовательностей нот. Будем считать, что $L0 = 1.$ По индукции докажем, что $Ln+1 ≥ Ln+ Ln−1$ для всех натуральных $n$ .

База индукции $(n= 1):$ $L2 = 4≥ 2+ 1= L1+ L0.$

Предположим, что неравенство $Lk+1 ≥Lk +Lk−1$ верно для всех $k$ , меньших $n.$ Покажем, что тогда $Ln+1 ≥ Ln+ Ln−1.$ Заметим, что

Ln+1 ≥2Ln − Ln−4− Ln−5− ...− L0

Действительно, мы можем добавить в конец ноту двумя способами к уже имеющейся незапрещенной мелодии из $n$ нот. При добавлении ноты могла возникнуть запретная мелодия длины $5$ в конце последовательности, однако она "испортит"максимум $L n−4$ последовательности нот, так как первые $n− 4$ ноты до "запрещенной"мелодии - незапрещенная мелодия длины $n − 4$ . Аналогично могли получить запретную последовательность из $6$ нот и испортить разрешённую мелодию из $n− 5$ нот и т. д. (Здесь мы можем вычесть лишнее, если $n> 30$ , и часть вычитаемых мелодий могут быть одинаковыми, но поскольку мы пишем оценку снизу, всё правильно.)

Из предположения индукции для $k< n$ $(Lk+1 ≥Lk +Lk−1)$ также следуют неравенства:

Lk+1− Lk ≥Lk−1

Lk+1− Lk−1 ≥Lk

Применим эти следствия, а также неравенство выше, для доказательства перехода индукции и получим:

Ln+1 − Ln − Ln−1 ≥(Ln− Ln−1)− Ln−4 − Ln−5− Ln−6− ...L0 ≥

≥(L − L )− L − L − ...− L ≥ L − L − L − ...L ≥ n−2 n−4 n−5 n−6 0 n−3 n−5 n−6 0

≥ Ln−4− Ln− 6− ...− L0 ≥...≥L1 = 2> 0

Следовательно, $Ln+1 ≥ Ln+ Ln−1$ и переход доказан.

Тогда из-за положительности $L0,L1$ последовательность $Ln$ возрастающая, а значит $L300 > 0$ , откуда следует, что Иван справится с испытанием Кощея.

Ответ: да

Курсы

Всё необходимое для достижения цели

Ошибка.
Попробуйте повторить позже

Задача 7#85489

В тетраэдре $ABCD$ скрещивающиеся рёбра попарно равны. Через середину отрезка $AH A$ , где $H A$ - точка пересечения высот грани $BCD$ , провели прямую $hA$ перпендикулярно плоскости $BCD$ . Аналогичным образом определили точки $HB, HC$ , $HD$ и построили прямые $hB,hC,hD$ соответственно для трёх других граней тетраэдра. Докажите, что прямые $hA,hB,hC,hD$ пересекаются в одной точке.

Источники: ММО - 2024, первый день, 11.5 (см. mmo.mccme.ru)

Подсказки к задаче

Подсказка 1.

Самый простой способ доказать, что несколько прямых пересекаются в одной точке - определить эту точку, а затем доказать, что все прямые через неё проходят. Попробуйте доказать, что данные прямые проходят через центр описанной сферы тетраэдра(точку O).

Подсказка 2.

Просто так работать с этим объектом не получается. Попробуем воспользоваться равенством скрещивающихся рёбер ABCD. Проведём через каждые пары скрещивающихся рёбер параллельные плоскости. Тогда какую фигуру мы получаем в качестве пересечения этих плоскостей?

Подсказка 3.

Да, верно! Это же прямоугольный параллелепипед! Тогда точка O является его центром(пусть A',B',C',D' - точки, симметричные A,B,C,D относительно O). Отметим точку пересечения медиан треугольника BCD (точка M). Попробуйте разложить векторы AM и AA' через векторы A'B,A'C,A'D.

Подсказка 4.

Мы получаем, что точка M лежит на AA' и A'M/AM = 1/2, то есть AO/OM = 3/1. Отлично! Теперь осталось доказать, что перпендикуляр, опущенный из O на BCD, проходит через середину AH(где H - ортоцентр треугольника BCD). Для этого рассмотрим проекцию на BCD(пусть A" - проекция A, O1 - проекция O). Мы знаем, что проекция прямой AM проходит через точку пересечения медиан и центр описанной окружности. Что же это тогда за прямая?

Подсказка 5.

Да это же прямая Эйлера! А значит, она проходит и через ортоцентр треугольника BCD. Теперь, используя, что MH = 2MO1, попробуйте получить отношение отрезков A"O1 и O1H.

Подсказка 6.

Отлично! Мы знаем, что A"O1 = O1H. Тогда что можно сказать про отношение отрезков, на которые разбивается AH прямой OO1?

Показать доказательство

Проведём через пару скрещивающихся рёбер тетраэдра $ABCD$ две параллельные плоскости. Так же поступим для двух других пар скрещивающихся рёбер и получим параллелепипед. Диагонали его граней равны между собой, поэтому все грани — прямоугольники, и параллелепипед прямоугольный. Пусть $O$ — его центр, являющийся также центром описанной сферы тетраэдра $ABCD.$ Пусть также $′ ′ ′ ′ A ,B ,C ,D$ — точки, симметричные $A,B,C,D$ соответственно относительно точки $O.$ Докажем, что все построенные прямые проходят через точку $O.$

$PIC$

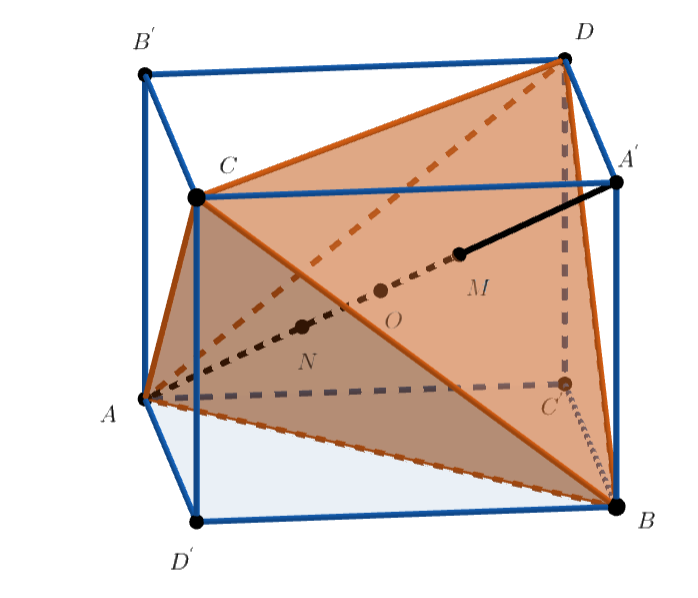
Пусть $M$ — центр масс треугольника $BCD$ . Тогда

−−−′→ 1−−′→ −−→′ −−→′ A M = 3(A B +A C +A D )

То есть точка $M$ лежит на диагонали $′ AA$ и делит её в отношении $2:1$ , считая от вершины $A.$ Аналогично центр масс $N$ треугольника $′ ′ ′ B CD$ лежит на этой диагонали и делит её в отношении $1:2$ , считая от вершины $A.$ Точка $O$ — середина отрезка $NM,$ поэтому $AO :OM = 3:1.$

$PIC$

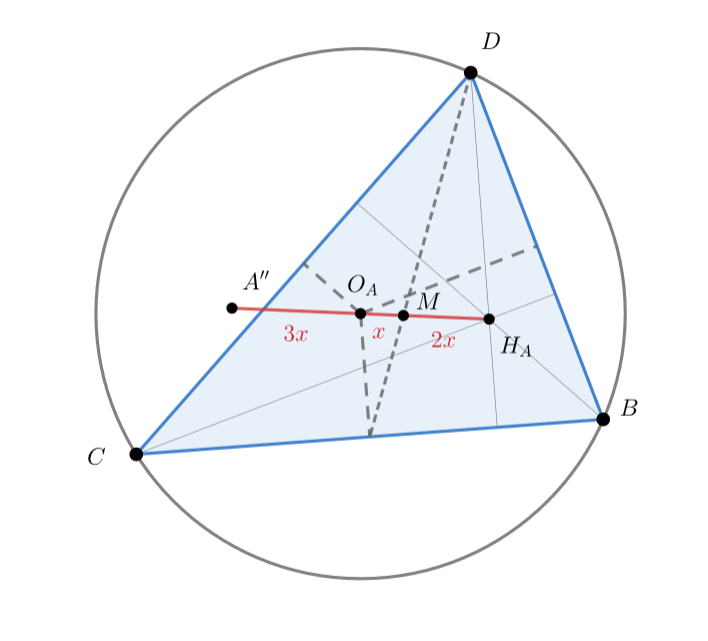
Рассмотрим проекцию на плоскость $BCD :$ $A ′′$ — проекция точки $A$ , $OA$ — проекция центра $O.$ Точка $O$ совпадает с центром описанной сферы тетраэдра $ABCD,$ поэтому $OA$ — центр описанной окружности треугольника $BCD.$

Тогда прямая $AA ′$ проецируется в прямую Эйлера $OAM$ треугольника $BCD.$ Пусть $OAM = x.$ Тогда $OAA ′′= 3x$ ( $O$ делит отрезок $AM$ в отношении $3:1$ , это отношение сохраняется при проецировании). Кроме того, $OA,M, HA$ лежат на одной прямой и $OAM :MHA = 1:2$ (прямая Эйлера), отсюда $MHA =2x.$ Следовательно, $OAA ′′ = OAHA$ , а прямая $OOA$ , перпендикулярная плоскости $BCD$ , делит отрезок $AHA$ пополам, а значит, совпадает с прямой $hA$ . Итак, все построенные прямые проходят через точку $O$ .

Ошибка.
Попробуйте повторить позже

Задача 8#85490

Дан многочлен степени $n ≥1$ с целыми ненулевыми коэффициентами, каждый из которых является его корнем. Докажите, что модули всех коэффициентов этого многочлена не превосходят 2.

Источники: ММО - 2024, первый день, 11.4 (см. mmo.mccme.ru)

Подсказки к задаче

Подсказка 1

Пусть Р(х) — многочлен из условия, а — его свободный член В этой задаче первым делом необходимо подумать, правда ли, что а делится на каждый из коэффициентов многочлена...

Подсказка 2

Да, это правда, так как это многочлен с целыми коэффициентами и каждый из коэффициентов является корнем. Нетрудно догадаться, что если свободный член по модулю меньше двух, то и остальные коэффициенты по модулю меньше двух. Тогда попробуйте доказать, что |a| < 2.

Подсказка 3

Это можно доказать по индукции. Не забудьте про базу при n = 1, а при переходе воспользуйтесь тем, что P(a) = 0.

Подсказка 4

Распишите Р(а) и вынесите а за скобочку. Пусть b — коэффициент при х в Р(х). Какой остаток тогда имеет b при делении на a? Чему в таком случае может быть равно b? Рассмотрите разные случаи, в одном из которых нужно будет не забыть про предположение индукции.

Показать доказательство

Пусть данный в условии многочлен с ненулевыми коэффициентами:

n P(x) =anx + ...a1x+ a0

По условию $ak$ — корень этого многочлена, где $k ∈{0,1,...,n}$ . И тогда:

n P(ak)= anak + ...+a1ak+ a0 = 0

Тогда $a0$ делится на все остальные коэффициенты многочлена $ak$ , а значит $|a0|≥|ak|> 0$ . Следовательно, достаточно проверить, что $|a0|< 2$ .

Докажем это по индукции по степени многочлена $n$ .

_________________________________________________________________________________________________________________________________________________________________________________

База индукции:

При $n =0 :P (a )= a = 0 0 0$ (чего не могло быть по условию). При $n =1 :$

P(a0)= a1a0+ a0 = 0 =⇒ a1 = −1

И тогда $P(x)=− x+ a0$ , а $P(a1)= 1+ a0$ , откуда $a0 = −1$ .

_________________________________________________________________________________________________________________________________________________________________________________

Переход индукции.

n n−1 P(a0)=ana0 + ...+ a1a0 +a0 = a0(ana0 + ...+ a2a0+ a1+1)

Так как $P(a0)=0$ и $a0 ⁄= 0$ , имеем $(anan0−1+ ...+ a2a0+ a1+ 1)=0$ . Тогда $a1+ 1$ делится на $a0$ . Как показано выше $a0$ делится на $a 1$ . Значит, $a + 1 1$ делится на $a 1$ , что возможно только при $a =±1. 1$

Если $a1 = 1$ , то $.. a1 +1= 2.a0$ , и утверждение доказано.

Если $a1 = −1$ , то преобразуем выражение дальше:

n−1 n−1 2 n−2 P(a0)= a0(ana0 + ...+ a2a0+ a1+ 1) =a0(ana0 + ...+ a2a0)= a0(ana0 + ...+ a3a0+ a2)

Опять-таки получаем, что

n−2 .. (ana0 + ...+ a3a0+ a2)=0 =⇒ a2 .a0

Тогда $a2 ...a0,a0...a2$ , что возможно только если $|a2|= |a0|$ . В случае если $a2 = a0$ , то мы пришли к выражению вида

n−2 n−3 G(a0)= bn−2a0 + bn−1a0 + ...+ a0b1+ a0 =0,

где $bi = ai+2$ , имеющее тот же вид, что и $P(a0)$ , но степени на $2$ меньшей. Из предположения индукции отсюда следует, что $|a0|≤ 2$ .

Если же $a2 = −a0$ , то домножим равенство на $− 1$ (эта операция не влияет на делимости коэффициентов и получим:

n−2 −ana0 − ...− a3a0+ a0 = 0

Для которого снова применимо предположение индукции, а значит $|a0|≤2$ .

Ошибка.
Попробуйте повторить позже

Задача 9#85492

Имеется кучка из 100 камней. Двое играют в следующую игру. Первый игрок забирает 1 камень, потом второй может забрать 1 или 2 камня, потом первый может забрать 1,2 или 3 камня, затем второй $1,2,3$ или 4 камня, и так далее. Выигрывает тот, кто забирает последний камень. Кто может выиграть, как бы ни играл соперник?

Источники: ММО - 2024, первый день, 11.3 (см. mmo.mccme.ru)

Подсказки к задаче

Подсказка 1

Давайте внимательно посмотрим на то, какое количество камней всегда может набрать первый игрок, после хода второго. Что можно заметить?

Подсказка 2

Первым ходом первый игрок всегда забирает ровно один камень, поэтому тут не очень интересно. А вот дальше второй игрок забирает один или два камня, а первый от 1 до 3 камней. Какое число камней можно набрать после хода второго и первого вместе?

Подсказка 3

Ровно 3 камня, на следующем ходе 5 камней, дальше 7 и так далее. То есть после хода первого получаются последовательные нечётные числа. А разность чего равняется последовательным нечётным числам?

Подсказка 4

Разность квадратов — это нечётное число. Поэтому, так как первым ходом первый игрок забирает 1 камень, то есть квадрат. А это значит, что после каждого его хода забирается такое количество камней, которое равно квадрату натурального числа!

Показать ответ и решение

Докажем, что для любого натурального $n≥ 10$ первый игрок на своём $n$ -ом ходе может добиться, чтобы количество забранных из кучки камней равнялось $2 n$ , и второй игрок не сможет ему помешать. Доказательство проведём индуктивно.

В свой первый ход первый игрок забирает один камень, т. е. число забранных камней равно $2 1$ . Пусть в свой $n$ -й ход первому игроку удалось сделать так, чтобы количество забранных камней равнялось $2 n$ . В свой $n$ -й ход второй игрок может взять от $1$ до $2n$ камней. Поскольку $2 2 (n +1) − n =2n +1,$ после его хода общее количество забранных камней будет больше $2 n$ и меньше $2 (n+ 1)$ . Первый игрок в свой следующий ход может взять от $1$ до $2n+ 1$ камня и точно сможет получить $2 (n+ 1)$ забранных камней независимо от предыдущего хода второго игрока.

Таким образом, поскольку $2 100= 10$ , побеждает первый игрок: ему достаточно каждый раз забирать такое число камней, чтобы общее число забранных камней было точным квадратом, и на своём $10$ ходе он возьмёт последний камень.

Ответ: первый

Ошибка.
Попробуйте повторить позже

Задача 10#85494

В остроугольном треугольнике $ABC$ проведена высота $AH$ . Точки $M$ и $N$ - середины отрезков $BH$ и $CH$ . Докажите, что точка пересечения перпендикуляров, опущенных из точек $M$ и $N$ на прямые $AB$ и $AC$ соответственно, равноудалена от точек $B$ и $C$ .

Источники: ММО - 2024, первый день, 11.2 (см. mmo.mccme.ru)

Подсказки к задаче

Подсказка 1

Пусть перпендикуляры через M и N пересекаются в точке P. Тогда над каким дополнительным построением можно подумать, чтобы сделать MP и NP чем-то хорошим? Не забудьте, что M и N являются серединами отрезков.

Подсказка 2

Да, давайте попробуем опустить перпендикуляры X и Y из точки H на стороны треугольника. В таком случае MP и NP являются средними линиями, так как они параллельны основаниям и делят одну из сторон пополам. Но как тогда можно переформулировать вопрос задачи удобным образом для нас?

Подсказка 3

Верно, это значит, что четырёхугольник CXYB должен быть вписанным, так как в таком случае P центр описанной окружности и равноудален от B и C. Теперь только осталось посчитать уголочки, используя вписанный четырёхугольник и равные углы в прямоугольном треугольнике с проведённой высотой. Победа!

Показать доказательство

Первое решение.

Обозначим точку пересечения перпендикуляров, опущенных из точек $M$ и $N$ на прямые $AB$ и $AC$ соответственно, через $P$ , а точки, симметричные $B$ и $C$ относительно прямых $MP$ и $NP$ , через $B0$ и $C0$ . Тогда прямые $MP$ и $NP$ — cерединные перпендикуляры к отрезкам $BB0$ и $CC0$ , поэтому достаточно доказать, что четырёхугольник $BB0C0C$ — вписанный.

$PIC$

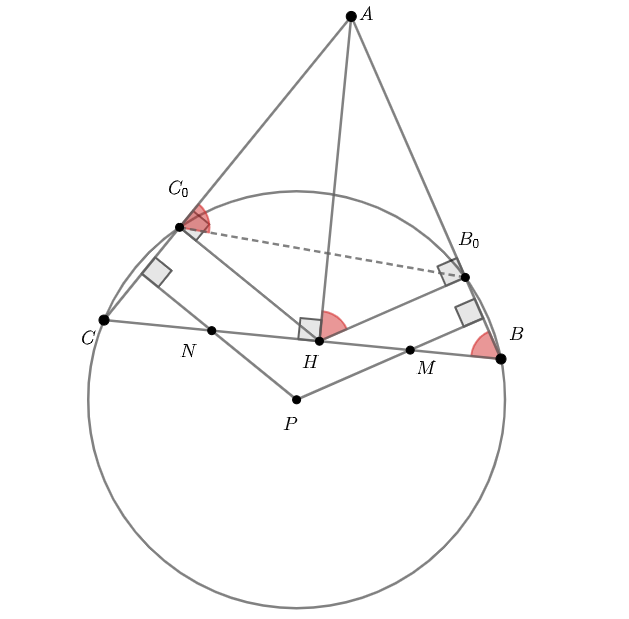
Заметим, что $MP$ и $NP$ содержат средние линии треугольников $BB0H$ и $CC0H$ , параллельные сторонам $B0H$ и $C0H$ соответственно. Значит, $HB0 ⊥ AB,HC0 ⊥ AC.$

Четырёхугольник $HB0AC0$ вписан в окружность, построенную на $AH$ как на диаметре, поэтому $∠B0C0A = ∠B0HA$ по свойству вписанных углов. При этом $∠B0HA =90∘− ∠HAB0 = ∠ABC$ . Значит, четырёхугольник $BB0C0C$ вписанный.

_________________________________________________________________________________________________________________________________________________________________________________

Второе решение.

Обозначим точку пересечения перпендикуляров, опущенных из точек $M$ и $N$ на прямые $AB$ и $AC$ соответственно, через $P$ , а точку пересечения высот треугольника $ABC$ — через $K$ .

$PIC$

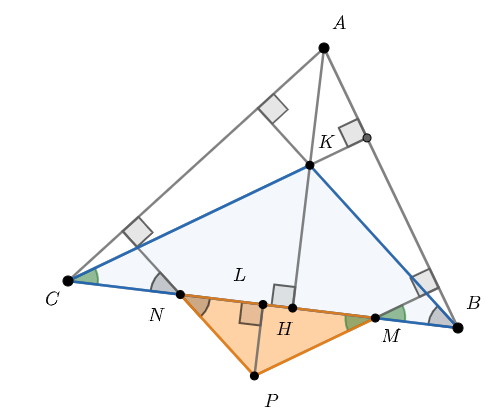
Тогда заметим, что треугольники $△BKC$ и $△NP M$ подобны по двум углам. Действительно, $∠MNP = 90∘− ∠BCA = ∠CBK$ . Аналогично, выполнено равенство $∠NMP = ∠BCK$ . Также заметим, что коэффициент подобия этих треугольников равен $2$ , поскольку $MBNC = 2$ .

Опустим из $P$ перпендикуляр $P L$ на $BC$ . Тогда из доказанного подобия следует, что $HLCM-= 2,$ т. е. $LM = NH$ . Следовательно, $BL = BM + ML = BM + NH = 12BC,$ а значит, $P$ лежит на серединном перпендикуляре к отрезку $BC$ , откуда следует требуемое.

Ошибка.
Попробуйте повторить позже

Задача 11#85495

У математика есть 19 различных гирь, массы которых в килограммах равны $ln2,ln3,ln 4,...,ln 20$ , и абсолютно точные двухчашечные весы. Он положил несколько гирь на весы так, что установилось равновесие. Какое наибольшее число гирь могло оказаться на весах?

Источники: ММО - 2024, первый день, 11.1 (см. mmo.mccme.ru)

Подсказки к задаче

Подсказка 1

Какие свойства есть у логарифмов? Что хочется применить в этой задаче, чтобы сравнивать не суммы логарифмов, а что-то другое?

Подсказка 2

Мы знаем, что сумма логарифмов равна логарифму произведения: ln(a) + ln(b) = ln(ab). То есть можно сравнивать не суммы логарифмов, а произведения их аргументов.

Подсказка 3

Теперь давайте каждое число разложим на множители, чтобы привести оценку и пример.

Подсказка 4

Большие простые числа (а именно те, которые больше 10) не могут быть в произведении.

Показать ответ и решение

Сумма логарифмов положительных чисел равна логарифму их произведения, поэтому будем уравнивать произведения двух непересекающихся наборов чисел из множества ${2,3,...,20}$ . Разложим натуральные числа от $2$ до $20$ на простые множители:

| | 3 | | | 2= 2 | 8 =22 | 14= 2⋅7 | | 3= 32 | 9 =3 | 15= 3⋅54 | | 4= 2 |10= 2⋅5 | 16= 2 | | 5= 5 | 11= 121 | 17= 172 | |6= 2⋅3 |12= 2 ⋅3 | 18= 2⋅3 2 | | 7= 7 | 13= 13 |19= 19,20= 2 ⋅5 |

Числа $11,13,17,19$ встречаются ровно по одному разу среди делителей, поэтому их следует исключить. Таким образом, на весах будет не более $15$ гирь.

Покажем, что можно уравновесить $15$ гирь. Приведем один из возможных примеров равенства произведений:

2⋅4⋅6⋅7⋅8⋅10⋅15⋅18 =

= 29⋅34⋅52⋅7= 3⋅5⋅9⋅12⋅14⋅16 ⋅20

Ответ: 15