СПБГУ 2022
Готовиться с нами - ЛЕГКО!
Ошибка.
Попробуйте повторить позже
На картинке нарисовано несколько кружочков, соединённых отрезками.
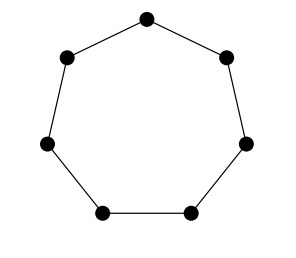
Саша выбирает натуральное число и расставляет в кружочках различные натуральные числа так, чтобы для всех этих чисел
выполнялось свойство: если числа
и
не соединены отрезком, то сумма
должна быть взаимно проста с
a если соединены, то
числа
и
должны иметь общий натуральный делитель, больший 1.
При каком наименьшем существует такая расстановка?
Источники:
Подсказка 1
Чтобы как-то снизить количество вариантов для n, давайте подумаем: а может ли n быть чётным?
Подсказка 2
Нет, поскольку если n чётно, то по принципу Дирихле найдутся два числа одинаковой чётности, которые не будет соединены! А значит их сумма кратна 2, поэтому НОД не будет равен 1. А теперь, зададимся вопросом: а могут ли три суммы четырех последовательно соединенных чисел быть кратны одному и тому же делителю числа n?
Подсказка 3
Нет, ведь в таком случае сумма крайних чисел(которые не соединены ребром) - тоже будет кратна этому делителю! То есть, число n не может равняться степени нечётного простого, поэтому оно кратно хотя бы двум различным нечётным простым! Теперь мы хотим взять минимальные простые(дли минимальности n), то есть, надо узнать, а может ли n быть кратно 3?
Подсказка 4
И опять-таки нет, n не может быть кратно 3. Поскольку, в таком случае найдётся пара чисел, соединенных ребром, сумма которых не будет кратна 3(для этого достаточно рассмотреть остатки при делении 3) То есть тройки не может быть среди простых! Осталось проверить, можно ли составить пример для n=5*7.
Сделаем два замечания.
1) нечетно. Действительно, пусть
четно. Среди семи чисел всегда есть три числа одной четности, и по условию они должны быть
попарно соединены. Но на картинке нет циклов длины 3.
2) Если — простой делитель
то среди четырех последовательно соединенных чисел существует пара соседних, сумма которых не
кратна
Возьмем цепочку
последовательно соединенных чисел. По условию
Тогда числа и
тоже соединены, то есть на картинке получился цикл длины 4, которого там нет.
Из 1) и 2) вытекает, что число имеет по крайней мере два различных нечетных простых делителя. Пусть их ровно два (скажем,
и
Покажем, что они отличны от 3. Допустим, например, что
Не более двух чисел делятся на 3 (если их три, то они образуют
цикл). Остальные числа разобьем на две группы, дающие при делении на 3 остатки 1 и 2. Одна из этих групп пуста, иначе любое число из
меньшей группы будет соединено по крайней мере с тремя числами из другой группы, что невозможно. Сумма чисел из одной группы на 3
не делится. Поэтому существует трехзвенная цепочка, в которой сумма любой пары соединенных чисел не кратна 3 и, значит, делится на
Но это противоречит 2).
Таким образом, если имеет ровно два различных нечетных простых делителя, то
Если же таких делителей больше
двух, то
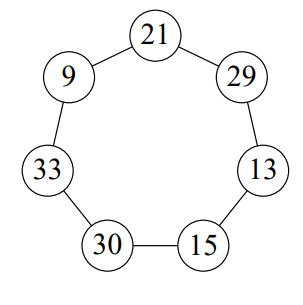
. Расстановка для
приведена на рисунке.
Ошибка.
Попробуйте повторить позже
При найдите максимальное значение выражения
Источники:
Подсказка 1
Для начала, давайте попробуем понять какой ответ, хотя бы на пальцах. Если мы увеличиваем х, то увеличивается значение, которое зависит от х, и в числителе, и в знаменателе, но при этом в числителе у нас степень функции больше трех, то есть, при х > 1 у нас числитель растет быстрее чем знаменатель. Все, что меньше единицы не очень понятно, но если мы верим в светлое будущее(то есть верим, что ответ достигается при х > 1) то нам надо посмотреть, чему равно значение дроби на всех двойках. И мы получим предполагаемый ответ. Теперь, когда мы знаем(а вернее - верим) в каких точках достигается ответ, то можно попробовать оценить как-то слагаемое в числителе, чтобы степень получившегося многочлена была равна 2(чтобы вероятно сократить с знаменателем), и при этом наша оценка достигалась именно в точке 2.
Подсказка 2
Корень можно оценить как <=2, так как х<=2(как раз в этой точке и достигается равенство). Второй множитель тогда можно оценить через 2х^2 - 6(опять же, равенство достигается в точке 2). Тогда, всю дробь можно оценить через (4(x^2 + y^2 + z^2) - 36)/(x^2 + y^2 + z^2). Ну а это уже достаточно легко оценить, зная, что все переменные меньше или равны 2.
Подсказка 3
Верно, выходит дробь 4 - 36/(x^2 + y^2 + z^2) <= 4 - 36/12 = 1. То есть, у нас есть оценка на дробь и при этом, мы так проводили неравенства, что каждое равенство в них достигалось в точке, в которой достигается итоговая оценка. Значит, у нас точно есть пример в котором это неравенство достигается. Запомните эту очень важную мысль, если у вас уже есть ответ и вы знаете в каких точках достигается равенство, то можно попробовать оценивать некоторые выражения, которые у вас есть так, чтобы равенство достигалось именно в той точке, где достигается равенство в изначальном выражении. Этот метод часто встречается на олимпиадах ИТМО, СПбГУ и других.
При справедливы неравенства
и
, откуда
Аналогичным образом оцениваются два других слагаемых в числителе Поэтому
Равенство реализуется при
Ошибка.
Попробуйте повторить позже
Диагонали вписанного четырехугольника пересекаются в точке
Внутри треугольника
выбрана такая точка
что
прямая
является биссектрисой угла
Луч
вторично пересекает описанную окружность треугольника
в точке
а
луч
вторично пересекает описанную окружность треугольника
в точке
Найдите отношение площадей треугольников
и
Источники:
Подсказка 1
Давайте попробуем найти какую-то связь между сторонами этих треугольников. Например: т.к. ABCD- вписан, то △BOC и △AOD подобны. Значит BO/AO=CO/DO. Что мы можем сказать про отношение CO/OD?
Подсказка 2
Мы видим, что в окружностях на CO и на OD смотрят одинаковые уголочки ∠CKO и ∠DKO => CO/OD=R₁/R₂, где R₁- радиус окружности, описанной около △COK, а R₂- радиус окружности, описанной около △DOK. Тогда BO/AO=R₁/R₂. А что мы можем сказать про отношение OL/OM?
Подсказка 3
Т.к. ∠LKO=180°-∠DKO=180°-∠CKO=∠MKO => LO/OM=R₁/R₂. Но тогда (BO*OM)/(AO*OL)=(R₁*R₂)/(R₂*R₁)=1. Мы знаем, что S(△BOM)=sin∠BOM*BO*OM/2 и S(△AOL)=sin∠AOL*AO*OL/2. Если мы докажем, что ∠BOM=∠AOL, то искомое отношение будет равно 1. Как это сделать?
Подсказка 4
Т.к. ∠OLK=∠OCK и ∠ODK=∠OMK, то треугольники △LOD и △MOC подобны по двум углам. А это значит, что ∠LOD=∠MOC. Осталось лишь докрутить это и понять, что ∠BOM=∠AOL и победа будет за нами!
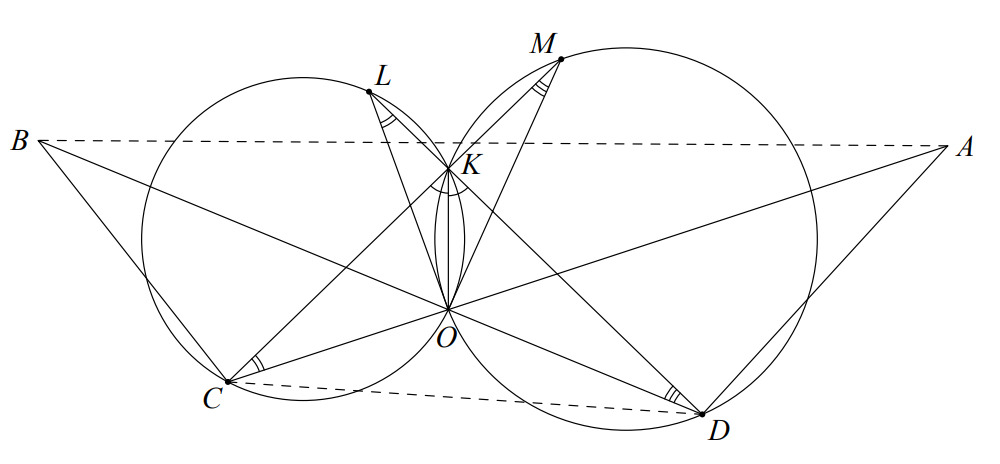
Пусть и
— радиусы окружностей, описанных около треугольников
и
соответственно. Заметим, что
откуда . Кроме того, из вписанности
вытекает, что треугольники
и
подобны по двум углам.
Тогда
так как хорды и
соответствуют одинаковым вписанным углам. Поэтому
Поскольку и
треугольники
и
подобны, откуда
Таким образом,
Ошибка.
Попробуйте повторить позже
Натуральное число в системе счисления с основанием
имеет вид
причем
Оказалось, что
-ичная запись
числа
представляет собой семизначный палиндром с нулевой средней цифрой. (Палиндромом называется число, которое читается
одинаково слева направо и справа налево). Найдите сумму
-ичных цифр числа
Источники:
Подсказка 1
Давайте потихоньку "причёсывать" задачу. Что даёт равенство из условия на числа p и q? Это значит, что мы можем записать p = 2s, а q = 5s, где s какое-то целое число. Попробуйте теперь записать x и x² в явном виде, учитывая условие с палиндромом. Получается ли там что-то относительно хорошее? Удобно ещё палиндром как-то обозначить.
Подсказка 2
Ага, получается, что после всех преобразований x= s (2r² + 5) (r + 1). Давайте обозначим палиндром abc0cba, где a, b, c соответственно какие-то цифры r - ичной системы. Тогда сгруппировав слагаемые в x² получится a(1 + r⁶) + b(r + r⁵) + c(r² + r⁴). Выходит нам нужно узнать сумму цифр, то есть 2(a+b+c). Давайте теперь приравняем два представления числа x². Учитывая, что у нас r - ичная система счисления, делимость на какое выражение тогда можно рассмотреть? Можете рассмотреть разные варианты и со временем придёте к нужному.
Подсказка 3
Верно, давайте рассмотрим делимость на (r + 1)², так как x² будет делиться на него, но нам интересна другая часть неравенства. Но появляется вопрос, как же находить остаток при делении степеней r на (r + 1)²? Попробуйте это понять, записав r^n = (1 + r -1)^n и раскрыв по биному Ньютона.
Подсказка 4
Ага, аккуратными вычислениями понимаем, что степень числа r даёт остаток (-1)^n (1-n (r+1)). Ничего страшного, если не получилось вывести, можете просто проверить по индукции, что это правда. Теперь попробуйте применить это к нашему выражению. Какой факт тогда можно понять про числа a, b, c?
Подсказка 5
Ага, из-за ограничения на a, b, c(они в r - ичной системе счисления) можно понять, что b = a + c. И раз мы узнали факт про b, то хорошо было бы тогда оценить именно его, чтобы потом сумму цифр легко найти. Поэтому попробуйте по аналогии посмотреть остаток при делении x² на 1 + r², а точнее сравнение. Там будет хорошо пописать неравенства для r и s, учитывая все ограничения, связанные с делимостью, системой счисления и количеством цифр.
Подсказка 6
Ага, для начала получаем, что r⩾6, и из сравнения, записав двойное неравенство для (9s² − b), будет следовать, что b = 9s². Далее останется только получить из верхнего ограничения для r, что s=1, а значит, b=9. Теперь осталось только посчитать правильно сумму цифр, и победа!
Договоримся писать если
Пусть
Тогда
Из условия на вытекает равенство
| (1) |
где — некоторые
-ичные цифры. Сделаем два наблюдения.
1) При любом натуральном
Левая часть кратна
откуда
Поскольку взаимно просто с
на
делится
Но это число лежит в интервале
откуда
2) Приравняем остатки левой и правой частей от деления на
Поскольку взаимно просто с
на
делится
Заметим, что
, иначе число
будет
восьмизначным. Кроме того,
. Поэтому
Таким образом,
Поскольку —
-ичная цифра, из 2) вытекает, что
, откуда
Так как
мы получаем
и
В силу
1) сумма цифр
равна
Замечание.
Прямым вычислением проверяется, что . Таким образом, описанная в условии ситуация реализуется.
Ошибка.
Попробуйте повторить позже
При каких клетчатую доску
можно разбить по клеточкам на один квадрат
и некоторое количество полосок из пяти клеток
так, что квадрат будет примыкать к стороне доски?
Источники:
Подсказка 1
Если так вышло, что мы смогли разрезать на квадрат 2*2 и полоски из 5 клеток, то что можно сказать про n? А если рассмотреть его по модулю 5? Тут неопытный читатель может спросить, почему именно 5? Это связано с тем, что мы как бы от нашего квадрата отрезаем полоски длины 5, значит, вычитаем каждый раз 5, и еще 5, и т.д. Значит, остаток mod 5 инвариантен. Поэтому именно по этому модулю надо рассматривать n.
Подсказка 2
Верно, что n² = 2² (mod 5), так как кол - во клеток с одной стороны это n² , с другой стороны - это сумма клеток квадрата и полосок по 5. Значит, либо n = 5k - 3, либо n = 5k + 3. Если верно последнее, то нужно еще проверить, что квадрат 2*2 примыкает к границе. Теперь, попробуйте как-то зафиксировать квадрат, то есть быть может как-то раскрасить и/или заполнить числами таблицу, чтобы числа в квадрате(цвета) были фиксированы. Иными словами, почему мы хотим так делать? Потому что у нас нет явного параметра, который сказал бы, что квадрат примыкает к таблице и мы хотим такой сделать. Что - то типа аналога координат.
Подсказка 3
Действительно, заполним первую строку единицами, вторую - двойками и т.д. Теперь нам надо посчитать по модулю 5 с двух сторон сумму чисел в таблице. Попробуйте это сделать и прийти к противоречию.
Подсказка 4
С одной стороны, так как сумма 5 подряд идущих строк кратна 5(просто потому что у нас в каждом столбце будут все остатки mod 5, а значит их сумма будет кратна 5, и таких столбцов n), а значит останутся только 3 первые строки, а сумма чисел в остальной таблице будет кратна 5. Значит, с одной стороны сумма чисел в таблице по модулю 5 - это n + 2n + 3n = n = 3 (mod 5). C другой стороны, если мы разрезаем на полоски длины 5 и квадрат, сумма в котором 1 + 1 + 2 + 2(так как он находится в первых двух строках. Ровно для этого мы и расставляли числа, чтобы зафиксировать наш квадрат где нужно) и равна 1 по модулю 5. Значит, пришли к противоречию, так как одинаковая величина имеет разный остаток при делении на 5. Значит, случай с n = 3 (mod 5) неразрешим. Остался n = 2 (mod 5). Тут уже вряд ли тоже ответ «нет», так как тогда вообще таких квадратов не бывает, но кажется такой квадрат можно подобрать, как минимум n = 2. Попробуйте для общего вида n = 2 (mod 5) привести пример.
Подсказка 5
Да, мы можем просто поставить квадрат 2*2 в левый верхний угол. Тогда, у нас оставшиеся две части первых двух строк и первых двух столбцов, по длине будут делиться на 5, а значит мы их можем разделить на полоски по 5. А с оставшейся частью таблицы что делать?
Если доску удалось разрезать на один квадрат
и некоторое количество полосок из пяти клеток, то
, откуда
дает остаток 2 или 3 от деления на 5. Предположим, что
и доску удалось разрезать требуемым образом.
Развернем ее так, чтобы квадрат примыкал к верхней стороне доски. Запишем в клетках верхней строки единицы, в клетках
следующей за ней строки — двойки, и так далее. Заметим, что сумма чисел в пяти последовательных строках кратна 5,
поскольку
Поэтому остаток от деления на 5 суммы всех расставленных чисел равен
С другой стороны, в каждой полоске сумма чисел кратна пяти, а в квадрате сумма чисел равна Значит, остаток от
деления на 5 суммы всех расставленных чисел равен 1 , и мы получаем противоречие.
Если то можно вырезать угловой квадрат
верхнюю полоску
разрезать на горизонтальные полоски из пяти
клеток, а прямоугольник
разрезать на вертикальные полоски из пяти клеток.
при

