Тема Иннополис - задания по годам

Иннополис 2021

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.
Готовиться с нами - ЛЕГКО!

Подтемы раздела иннополис - задания по годам

Решаем задачи

Ошибка.
Попробуйте повторить позже

Задача 1#94950

Решите уравнение:

log25(x − 500)− logx 25 =1.

Источники: Иннополис - 2021, 11.1 (см. dovuz.innopolis.university)

Показать ответ и решение

Заметим, что допустимыми являются лишь $x >500$ .

log25(x − 500)= 1+logx 25.

Левая часть равенства с ростом $x$ возрастает, а правая - убывает. Значит, уравнение имеет не более одного корня, и этот корень можно угадать.

Ответ:

$625$

Бандлы и наборы

Комбо-тарифы сразу по нескольким предметам

Ошибка.
Попробуйте повторить позже

Задача 2#94951

Дан треугольник $ABC$ . Существует единственный набор таких трёх окружностей $ω ,ω A B$ и $ω C$ , которые лежат внутри треугольника, попарно друг друга касаются, а также каждая из них касается сторон соответствующего угла: $ωA$ касается сторон $AB$ и $AC,ωB$ касается сторон $BA$ и $BC,ωC$ касается сторон $CA$ и $CB$ .

Обозначим точку касания окружностей $ωA$ и $ωB$ как $TAB$ . Аналогично определяются точки $TAC$ и $TBC$ .

Дизайнер хочет сконструировать люстру-витраж из цветного стекла, в которой стороны треугольника $ABC$ - это прочный (пренебрежимо) лёгкий контур, в который вписан массивный плоский диск весом 1 кг, а также добавлены уравновешивающие веса в вершинах $A,B$ и $C$ треугольника так, чтобы точка подвеса люстры находилась на пересечении отрезков $ATBC,BTAC$ и $CTAB$ (остальные детали люстры имеют пренебрежимо малый вес). Докажите, что такой проект люстры осуществим и определите уравновешивающие веса в вершинах (то есть такие, чтобы люстра висела горизонтально, закреплённая только в точке подвеса), если радиусы окружностей $ω$ - это $rA,rB,rC$ , а радиус вписанного диска треугольника равен $r$ .

Источники: Иннополис - 2021, 11.2 (см. dovuz.innopolis.university)

Показать доказательство

Обозначим массы в вершинах $A,B$ и $C$ соответственно как $m ,m A B$ и $m C$ . Докажем, что массы $m = 0.5(r−rA),m = 0.5(r−-rB),m = 0.5(r−rC) A rA B rB C rC$ подходят.

$PIC$

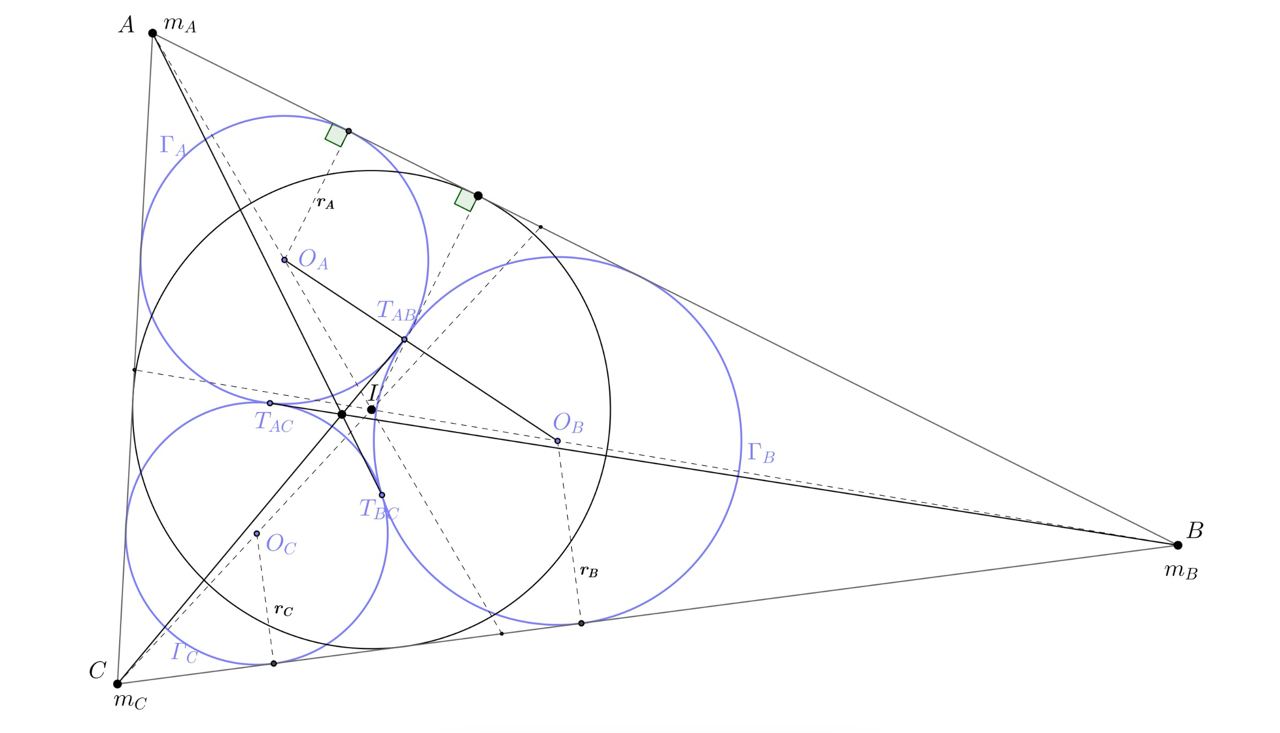
Покажем, что центр масс системы нагруженных точек $(A,mA ),(I,0.5$ кг) находится в точке $OA$ - центре окружности $Γ A(X)$ (см. рисунок). Из подобия соответствующих прямоугольных треугольников вытекает, что $AI :AOA = r:rA$ . Тогда $IOA∕AOA = (r− rA)∕rA$ . Чтобы точка $OA$ была центром масс указанных точек, по правилу рычага, должно выполняться $0.5⋅IOA = mA ⋅AOA$ . Подставив указанное значение для $mA$ , легко видеть, что правило рычага выполняется и для пары точек $(A,mA ),(I,0.5)$ (и центра масс $OA$ ), и для пар точек $(B,mB ),(I,0.5)$ и $(C,mC ),(I,0.5)$ с центрами масс $OB$ и $OC$ соответственно.

Тогда, пользуясь принципом перегруппировки масс, имеем, что центр масс системы точек $(I,1),(A,mA ),(B,mB)$ и $(C,mC )$ совпадает с центром масс системы точек $(I,0.5),(OA,0.5+mA ),(B,mB )$ , что совпадает с центром масс системы $(OA,0.5+mA ),(OB,0.5+mB ),(C,mC )$ .

Но $0.5 +mA = 1+ r−rA =-r- 2 2rA 2rA$ . Аналогично, $0.5+ mB = -r- 2rB$ и $0.5+ mC = -r- 2rC$ . Значит, указанная система нагруженных точек переписывается в виде $( -r-) ( -r-) OA,2rA , OB,2rB ,(C,mC )$ .

Окружности $Γ A (OA)$ и $Γ B(OB)$ , по выбору, касаются. Значит, отрезок $OAOB$ равен по длине $rA +rB$ и делится точкой $TAB$ на части длины $rA$ и $rB$ . Но тогда для точек $( r-) ( r-) OA, 2rA , OB, 2rB$ и точки $TAB$ выполняется равенство $-r------- -r------- 2rA OATAB +2rBOBTAB = 0$ . Значит, $TAB$ - центр масс системы из этих двух точек, а значит, центр масс изначальной системы $(I,1),(A,mA),(B,mB)$ и $(C,mC)$ , после перегруппировок, совпадает с центром масс системы двух точек: $( -r- -r-) TAB,2rA + 2rB ,(C,mC )$ . Как следствие, этот центр масс лежит на отрезке $TABC$ . По абсолютно аналогичным причинам, центр масс изначальной четвёрки нагруженных точек лежит также на отрезках $BTAC$ и $CTAB$ . Таким образом, выбранные веса $mA,mB, mC$ удовлетворяют требованию задачи.

Ошибка.
Попробуйте повторить позже

Задача 3#94952

Дан клетчатый прямоугольник $2m ×2n$ , разбитый произвольным образом на доминошки $2× 1$ .

Если две доминошки образуют квадрат $2× 2$ , разрешается повернуть их обе на $∘ 90$ (сделать флип). Наша цель — последовательностью флипов сделать все доминошки горизонтальными (кирпичная кладка) за как можно меньшее количество операций.

Раскрасим наш прямоугольник в шахматную раскраску, считая левый нижний угол черным. Направим по сторонам квадратиков стрелочки так, чтобы черные квадратики обходились бы против часовой стрелки, а белые — по часовой стрелке.

Пусть нам дано некоторое замощение прямоугольника доминошками, которое мы обозначим через T. Сопоставим замощению его функцию высоты — это будет функция на вершинах клеток нашего прямоугольника, которую мы будем обозначать $HT (v)$ .

Определим её следующим образом. Выберем левую нижнюю вершину $v0$ прямоугольника и положим ее высоту равной нулю; далее, каждую вершину $v$ соединим с $v0$ путем, который проходит по линиям сетки и не пересекает доминошек. Этот путь состоит из стрелок, каждая из которых проходится либо в попутном направлении (т. е. сонаправлена с путем), либо в противоположном. Положим высоту $HT(v)$ равной разности числа попутных и противоположно направленных стрелок.

Назовем кирпичной кладкой разбиение $Tmin$ , в котором все доминошки горизонтальны. Назовем приведенной высотой разбиения $T$ величину

| | hT(v)= |HT(v)− HTmin(v)|. 4

Назовём рангом замощения $T$ число $r(T)=∑v hT(v)$ . Докажите, что любое замощение $T$ можно превратить в кирпичную кладку за $r(T)$ флипов, причём за меньшее количество флипов это сделать невозможно.

Источники: Иннополис - 2021, 11.3 (см. dovuz.innopolis.university)

Показать доказательство

Утверждение. Функция высоты $H T$ задаёт разбиение единственным образом.

_________________________________________________________________________________________________________________________________________________________________________________

Доказательство. Покажем, что для любых соседних вершин $u$ и $v,$ ребро между которыми направлено от $u$ к $v,$ либо $HT (v)= HT(v)+1,$ либо $HT (v)= HT(u)− 3$ . Действительно, первый случай реализуется, когда стрелка от от $u$ к $v$ — это стрелка на границе доминошки, а второй случай сотвествует тому, что это стрелка, которая разделяет доминошку на две половинки.

Рассмотрим те рёбра, разность функций высоты на концах которых равна $1$ . Эти рёбра будут образовывать границы доминошек нашего разбиения; напротив, те ребра, разность функций высоты на концах которых равна $− 3$ , будут «закрыты» доминошками. Далее рассмотрим какую-нибудь клетку. Все стрелки на её границе направлены в одном направлении: либо по часовой стрелке, либо против. Поскольку сумма приращений функции высоты при обходе этой клетки равна нулю, это значит, что существует ровно три ребра из четырех, для которых разность значений функции высоты на их концах равна единице, и одно ребро, для которого эта разность равна минус трём; оно и будет закрыто доминошкой. То же самое можно будет сказать и про клетку, смежную с данной по этому ребру. Тем самым все клетки окажутся разбитыми на пары, то есть в итоге из функции высоты действительно однозначно получится замощение нашего прямоугольника.

_________________________________________________________________________________________________________________________________________________________________________________

Будем вести индукцию по величине $r(T)$ .

Если $r(T)= 0$ , доказывать нечего, т.к. тогда $HT = HTmin$ , и, согласно утверждению выше, $T = Tmin$ . В противном случае рассмотрим в замощении $T$ функцию $|HT |$ , пусть $v1$ — вершина, в которой эта функция достигает глобального максимума (если таких вершин несколько, выберем любую из них). Заметим, что в этой вершине можно сделать флип. Действительно, рассмотрим квадрат $2× 2$ , центром которого является вершина $v1$ . Тогда или горизонтальные, или вертикальные ребра, выходящее из $v1$ , должны быть закрыты доминошками разбиения $T$ (если из вершины $v1$ выходит и горизонтальное, и вертикальное ребра, то, сдвинувшись по одному из них, можно увеличить значение $|HT (v1)|$ , что невозможно, т.к. $v1$ — точка максимума). Значит, квадрат $2× 2$ действительно разбит на две доминошки, и флип возможен.

Сделаем флип с центром в этой точке. Данный флип уменьшит приведеную высоту вершины $v1$ на $1,$ а высоты остальных вершин оставит без изменений. Так мы получим новое замощение $T′$ , для которого $r(T′) =r(T)− 1$ . Применяя предположение индукции, получаем требуемое.

Ошибка.
Попробуйте повторить позже

Задача 4#95205

Дана система уравнений, описывающая положение и ориентацию исполнительного механизма робота на плоскости вида

(| x= a⋅cos(ϕ )+b⋅cos(ϕ + ϕ )+c ⋅cos(ϕ +ϕ + ϕ ) { y = a⋅sin(ϕ1)+b⋅sin(ϕ1+ ϕ2)+ c⋅sin(ϕ1+ ϕ2+ϕ 3) |( 1 1 2 1 2 3 γ = ϕ1+ ϕ2+ϕ3

Найдите конфигурацию ( $ϕ1,ϕ2,ϕ3$ ) для заданного положения и ориентации $(x,y,γ)$ , а также известных $a,b,c$ . При каких $a,b,c$ задача имеет решение?

Источники: Иннополис - 2021, 11.4 (см. dovuz.innopolis.university)

Показать ответ и решение

$PIC$

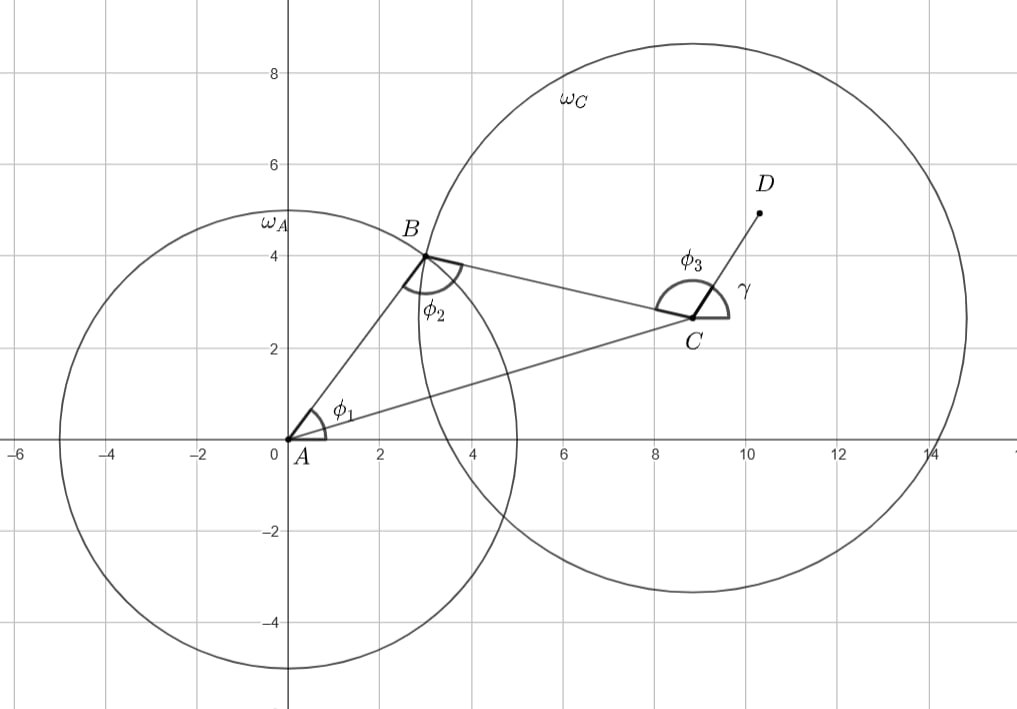
Изобразим на координатной плоскости трехзвенный манипулятор (звенья длин $|a|,|b|,|c|)$ , первое звено $AB$ которого — отрезок с началом в $A(0,0)$ , а третье — отрезок с концом $D(x,y)$ . Тогда $ϕ1$ — угол, образованный первым звеном и осью $x,ϕ2$ и $ϕ3$ — углы соответственно между первым и вторым, и вторым и третьим звеньями манипулятора, а $γ$ — угол между направленным третьим звеном и положительным направлением оси $x.$

Изобразим окружности $ωA$ и $ωD$ с центрами в точках $A$ и $D$ и радиусами $|a|$ и $|c|$ соответственно. Вектор $−C−→D$ (третье звено манигулятора) образует известный угол $γ$ — таким образом, точка $C$ имеет координаты $(x− c⋅cosγ;y− c⋅sinγ)$ . Изобразим окружность $ωC$ с центром в точке $C$ и радиусом $|b|.$

$PIC$

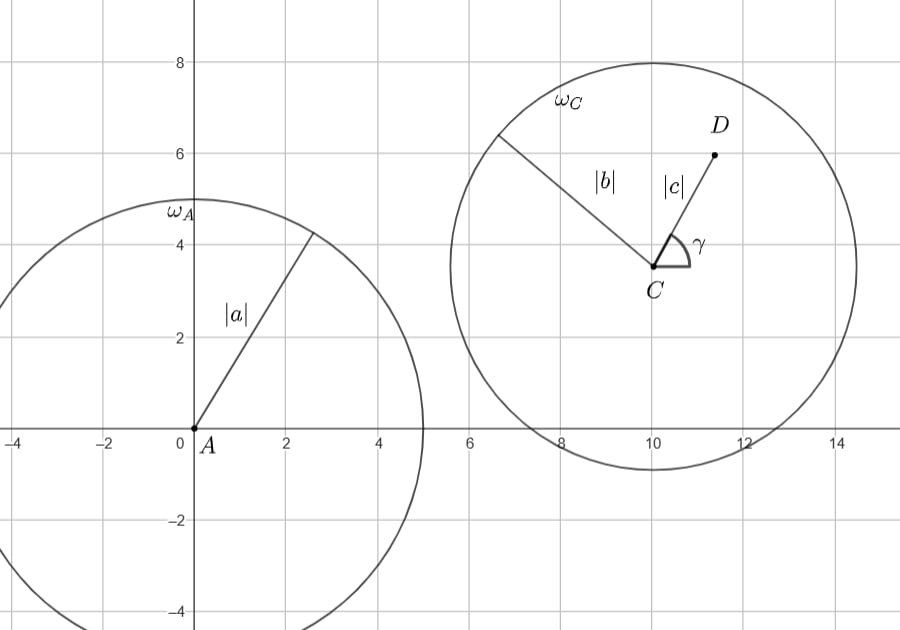
Количество общих точек окружностей $ωA$ и $ωC$ равно количеству решений задачи. Задача не имеет решений, если треугольника (пусть и вырожденного) со сторонами $|AC |,|a|,|b|$ не существует.